問 題
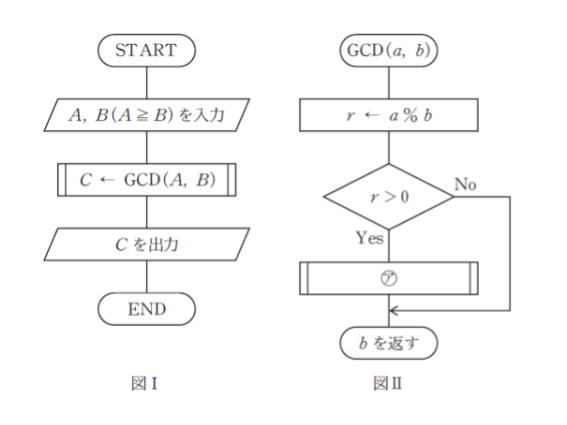
図は、ユークリッドの互除法を用いて二つの任意の自然数 A, B (A ≧ B) の最大公約数を求めるフローチャートであり、図Ⅰがメインルーチン、図Ⅱがサブルーチンである。サブルーチンのフローチャートでは以下の性質を用いている。
「二つの自然数 a,b (a≧b) について a を b で割ったときの余りを r とおくと、r が0より大きいならば a と b の最大公約数は b と r の最大公約数と等しくなり、r が0ならば b が最大公約数である。」
このとき図中の ㋐ に当てはまるものとして最も妥当なのはどれか。なお図中の % は剰余演算子であり a % b は a を b で割ったときの余りである。
1. b ← GCD (b , r)
2. b ← GCD (r , b)
3. b ← GCD (a , b)
4. b ← r
5. b ← a
正解 (1)
解 説
A = 91,B = 21 を例にチャートを読んでいきます。(適当な具体例です。)
GCD(91,21) を呼び、サブルーチンのチャートに移ります。 r に 91 ÷ 21 = 4・・・7なので、7 を代入します。ここで 91,21 の公約数と 21,7 の公約数が一致です。 r > 0 なので、yes で ㋐ にいくため、「21 と 7 の最大公約数を探す」ような記述を入れたいところです。つまり GCD(21,7) 呼び出しです。これに該当するのは、選択肢 1 です。
以上より、正解は 1 です。

コメント