問 題
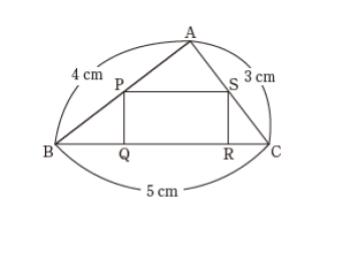
AB = 4 cm、BC = 5 cm、CA = 3 cm の三角形がある。この三角形に図のように長方形PQRSを内接させる。長方形 PQRS の面積が最大となるときの辺 PQ の長さはいくらか。
1.1 cm
2.6/5 cm
3.3√3 /4 cm
4.3/2 cm
5.25/12 cm
解 説
3cm,4cm,5cm の三角形なので、直角三角形です。これは基礎知識です。また、見える三角形はすべて相似なので、辺の比が 3:4:5 となります。
問われているのが PQ なので、PQ(=SR) の長さを x とおきます。長方形 PQRS の面積を考えるためには PS ( = QR) の長さが必要になります。
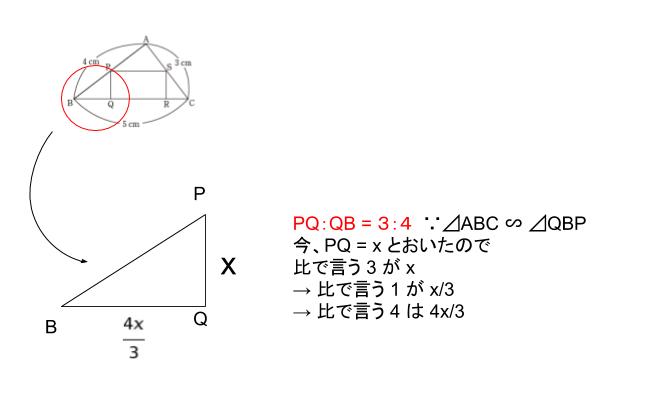
ここで、⊿BPQ に注目します。辺の比は、PQ:QB:BP = 3:4:5です。比で言う3の所が x です。従って、比で言う1が、x/3 と表されます。よって、QB は比で言う4なので、4x/3 です。下図のようになります。
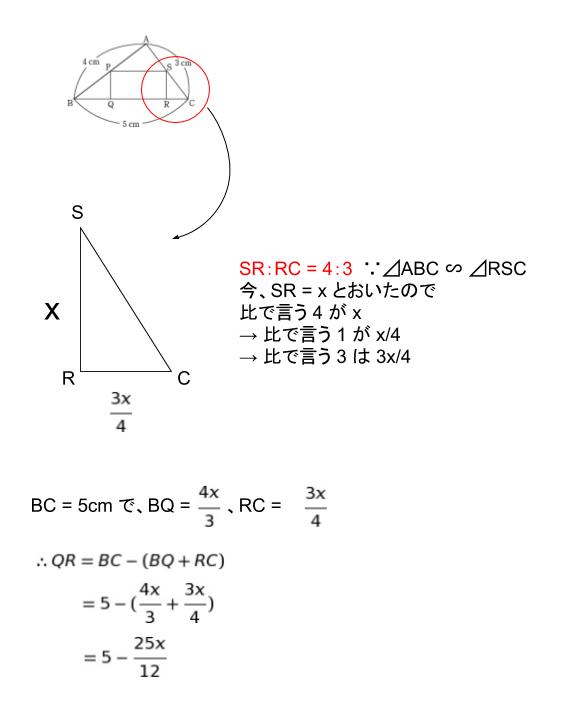
同様に、⊿CRS に注目すると、SR:RC = 4:3です。比で言う 4 が x なので、比で言う 1 が x/4 です。従って、RC = 3x/4 と表すことができます。以上より、QR = 5-(4x/3 + 3x/4)です。分数部分を計算すると、QR = (5-25x/12)です。下図のようになります。
長方形の面積が x × (5ー25x/12) = 5x ー 25x2/12 と表されることがわかりました。選択肢を代入して大小関係を考えてもよいのですが、選択肢 3 の評価が難しくなるため、微分するのがおすすめです。微分した式 = 0 となるような x を選択肢から探せば OK です。
f(x) = 5x ー 25x2/12 とおけば
f’(x) = 5 – 50x/12 = 5-25x/6 となります。
f’(x) = 0 となる x を選択肢から選べば x = 6/5 です。
よって正解は 2 です。

コメント