問 題
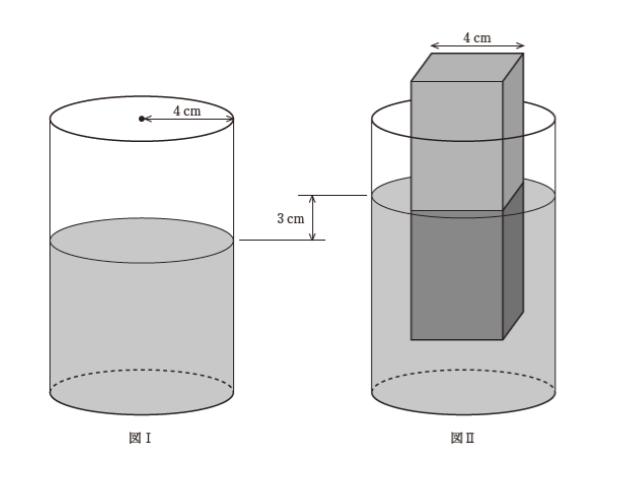
図Ⅰのように、底面の半径が 4cm の円筒に、ある高さまで水が入っている。いま、図Ⅱのように、一辺の長さが 4cm の正方形を底面とする四角柱を、底面を水平に保ったままこの水中に沈めていったとき、水面の位置が 3cm 高くなった。このとき、四角柱の水につかっている部分の高さはいくらか。
1.3π ー3 cm
2.4π ー4 cm
3.3π cm
4.3π +3 cm
5.4π cm
正解 (3)
解 説
「四角柱が押しのけた水」が、水面を3cm押し上げています。
四角柱が押しのけた水と、押しのけられた水の関係は以下の通りです。
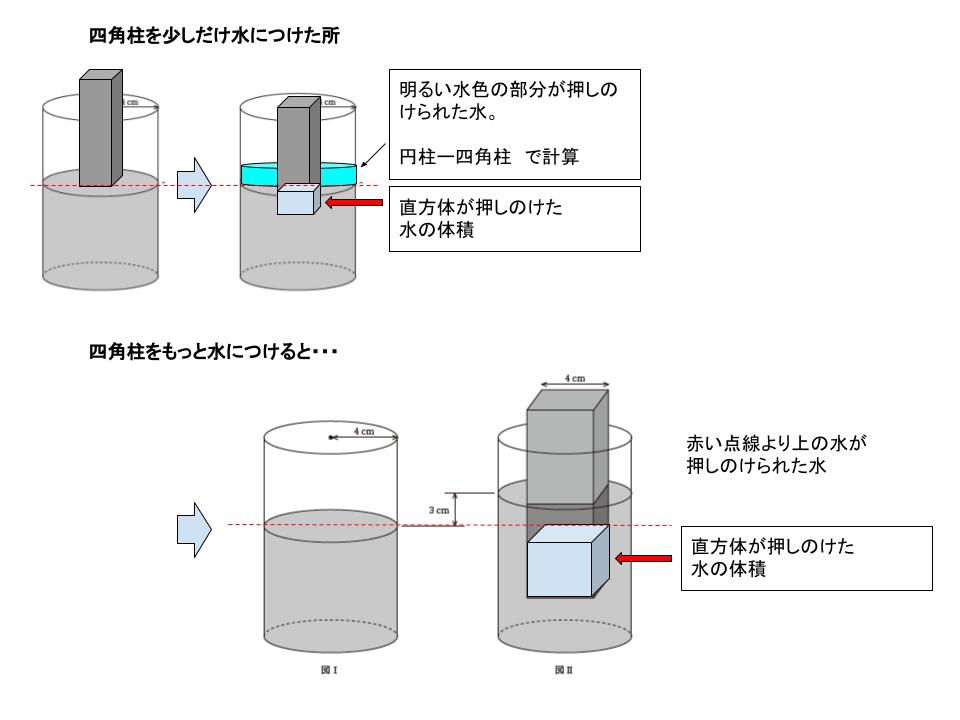
図Ⅱにおいて水に浸かっている部分の高さを x cm とします。四角柱が押しのけた水の体積は、16(x-3) です。
そして、押しのけられた水の体積は、赤い点線よりも上の部分なので「3cm 分の円柱 ー 3cm 分の四角柱」です。3cm 分の円柱は 48π cm3 、3cm 分の四角柱は 48 cm3 です。
従って、16(x-3) = 48πー48 が成り立ちます。解くと、x = 3 π です。
以上より、正解は 3 です。

コメント