問 題
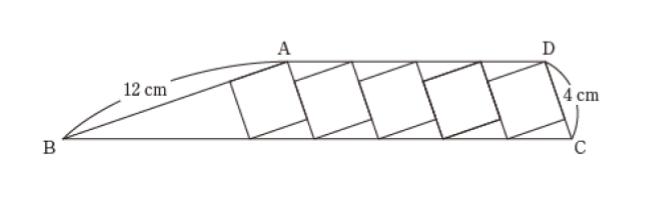
図のように、同じ大きさの正方形 5 個を並べ、両端の正方形の一辺を延長した直線と各正方形の頂点を通る直線を結んで台形ABCD を作ったところ、辺 AB の長さが 12 cm、辺CD の長さが 4 cm となった。このとき、台形ABCD の面積は正方形 1 個の面積の何倍となるか。
1.7 倍
2.7.5 倍
3.8 倍
4.8.5 倍
5.9 倍
正解 (3)
解 説
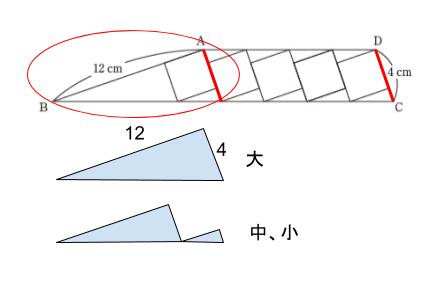
図の中に見える AB を斜辺とする直角三角形を「大」、大の一部として、Bを含む三角形を「中」、右下部分にできる小さな三角形を「小」と名付けます。大の直角を構成する2辺の長さは 12cm,4cm です。
大、中、小は明らかに相似なので、直角を構成する2辺の比は、全て12:4 = 3:1です。(下図参照)
正方形の一辺の長さを x とおくと、「小」の直角三角形に注目して、以下のように辺の長さを x を用いて表すことができます。
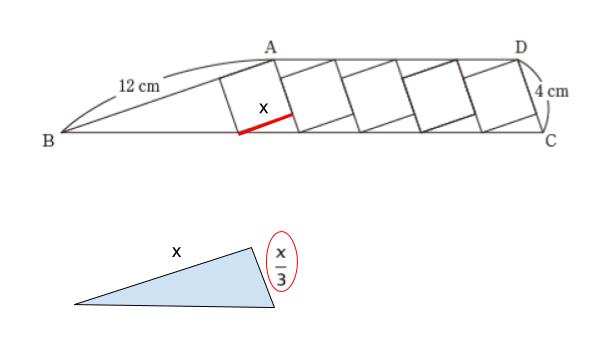
すると、正方形の一辺は「4 ー x/3」とも表されます。 従って、x = 4-x/3 です。これを解くと、x = 3 です。正方形1個の面積は 3×3 = 9 とわかります。
台形の面積は、「大×1+小 × 8 +正方形 × 4」 です。大の面積は 1/2 × 12 × 4 = 24 です。小1個の面積は 1/2 × 3 × 1 = 3/2 です。8個ならば 3/2 × 8 = 12 です。正方形 4 個は 9 × 4 = 36 です。すべてあわせると 24+12+36 = 72 です。
72 ÷ 9 = 8 なので、台形の面積は、正方形 1 個の面積の 8 倍となります。正解は 3 です。

コメント