公務員試験 H25年 国家一般職(土木) No.4解説

　問 題　　　　　

以下の定積分はいくらか。

1. -2
2. -1
3. 0
4. 1
5. 2

 

 

 

 

 

　解 説　　　　　

【解法１　部分積分で計算】

xcosx = x(sinx)’ とみて部分積分で計算すれば、不定積分の結果が

xsinx – ∫sinx
= xsinx + cosx です。

x = πを代入すると -1、x = 0 を代入すると 1 なので、－１－１＝－２となります。

従って、正解は 1 です。

【解法2 面積評価】

部分積分の公式を忘れた場合も面積評価で正解を絞る頃ができます。

x = 0,π/2、の時、xcosx = 0 です。

x = π/4 の時、xcosx = π/4 × √2/2 です。π≒ 3.1,√2 ≒ 1.4 と近似すればπ/4 × √2/2 は大体 0.8 × 0.7 ≒ 0.56 です。

x = 3π/4 の時、xcosx = 3π/4 × (-√2/2) です。やはり近似すれば大体 2.4 × -0.7 ≒ -1.7 です。

x = πの時、xcosx = πです。

5点を やや cosx を意識して滑らかにつなぐと以下の図のようになります。曲線部分を直線とみなし大体の三角形として計算すると右部分のようになります。

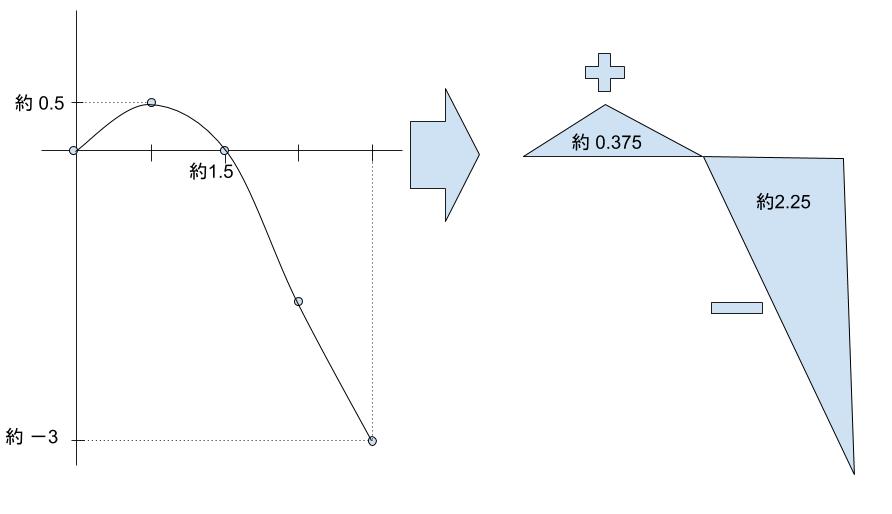
従って、一番近いのは　－２です。

以上より、正解は 1 です。