公務員試験 H25年 国家一般職(電気・電子・情報) No.23解説

　問 題　　　　　

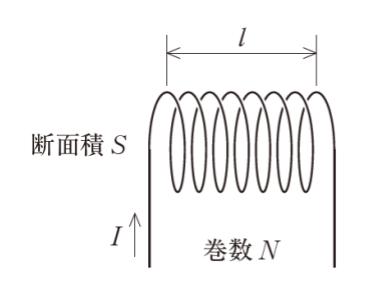
図のように、真空中に置かれた断面積 S、長さ l、巻数 N の十分に長い理想的な円形コイルに、電流 I が流れている。このとき、コイル内部の磁束密度は μ₀NＩ/ l と表される（μ₀ は真空の透磁率）。このコイルの自己インダクタンス L に関する記述として最も妥当なのはどれか。

1. S のみを 4 倍にしたとき、L は 2 倍になる。
2. S のみを 2 倍にしたとき、L は 2 倍になる。
3. N のみを 4 倍にしたとき、L は 2 倍になる。
4. N のみを 2 倍にしたとき、L は 2 倍になる。
5. l のみを 2 倍にしたとき、L は変わらない。

 

 

 

 

 

　解 説　　　　　

磁束密度を「B」とおきます。問題文よりコイル内部の磁束密度が B = μ₀NＩ/ l　・・・（１） です。ここで「N/l」は単位長さあたりの巻き数を表しています。巻数 N のコイルにおいて生じる誘導起電力は V = N(dΦ/dt) です。（ファラデーの法則）

一方、自己インダクタンスの定義は、「誘導起電力」を「電流の変化（dI/dt）」×比例定数（L）と書き直した時の「比例定数」です。与えられているのが、磁束密度（B)なので、まずそれを磁束（Φ）にするため S をかけます。
Φ = BS = S μ₀NＩ/ l です。

巻数 N のコイルなので、ファラデーの法則より
V = N(dΦ/dt) = N(d/dt)(S μ₀NＩ/ l) です。S,μ₀,N,l は定数なので
= N²Sμ₀/l (dＩ/dt) となります。 従って、自己インダクタンス L は μ₀ N²S/l です。

つまり
・S を 2 倍にしたとき、L 2 倍。
・N を 2 倍にしたとき、L 4 倍。
・l を 2 倍にした時、L = 1/2 です。

以上より、正解は 2 です。