問 題
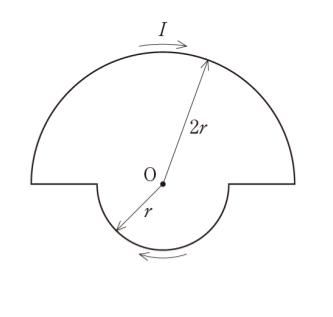
図のように、直線導線と点Oを中心とした半径 r 及び半径 2r の二つの半円形導線からなる回路に、電流 I を流したとき、点Oにおける磁界の大きさとして最も妥当なのはどれか。
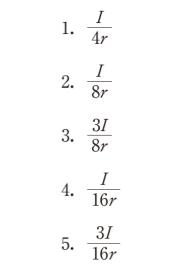
解 説
電流と、離れた点の磁界の大きさ と来たら BiotーSavart(ビオ・サバール)の法則です。電流が流れる導線の微小区間を ds, 変位 r のなす角を θ とするとき、その大きさが dH = I/4π × ds sinθ/ r2 です。
問題文の図は、「直線導線」と「半円形導線」でできているので、それぞれの部分に分けて考えます。直線導線では、ビオ・サバールの法則より dH = 0 となるので、磁界の大きさはありません。
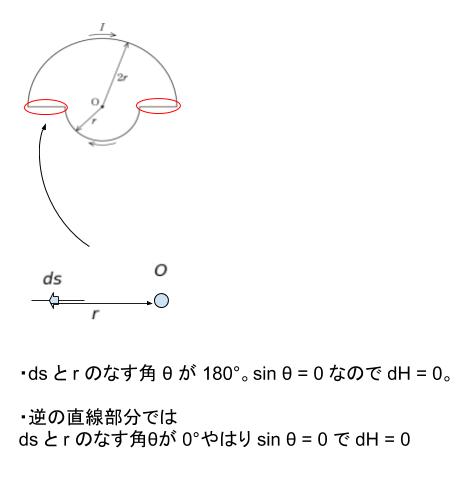
半円形電流による磁界の大きさですが、「半径 a 中心角 α の弧に電流 I が流れる」時、中心 O に生じる磁界はビオ・サバールの法則において、r = a, θ = π/2 (円の接線方向と中心を結べば必ず直角なので)とすれば、dH = Ids/4πa2 です。
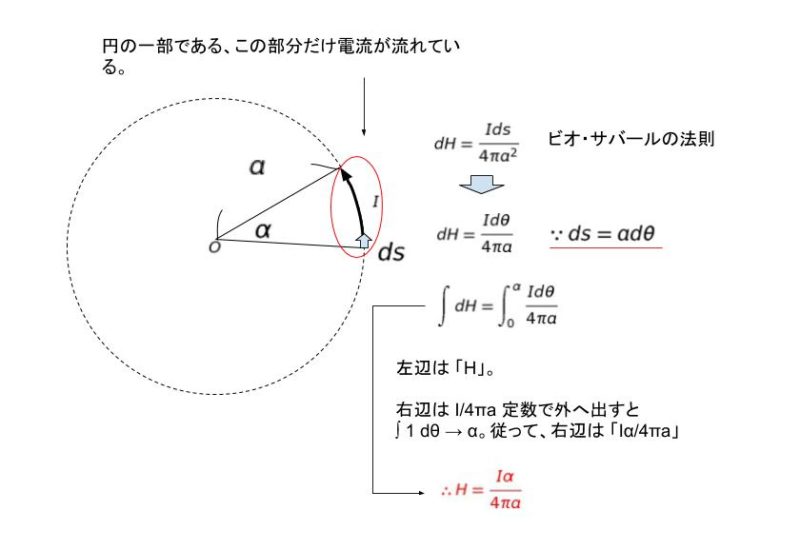
円の弧長は、中心角をラジアン表記すると、l = rθ なので、本問では弧長を adθ と表すことができます。従って、ds = adθを代入し、θ = 0 ~ α まで積分すればOKで、計算結果が H = Iα/4πa です。(これを覚えておいて、いざとなれば導く とすると役立つ知識と思われます。)
従って、半円形導線部分については、「H = Iα/4πa」において、半径 r の方は a = r, α = π を代入すれば OK です。すると 「I/4r」 です。半径 2r の方は、a = 2r,α = π を代入すれば、「I/8r」 です。I/4r + I/8r = 3I/8r です。
以上より、正解は 3 です。

コメント