問 題
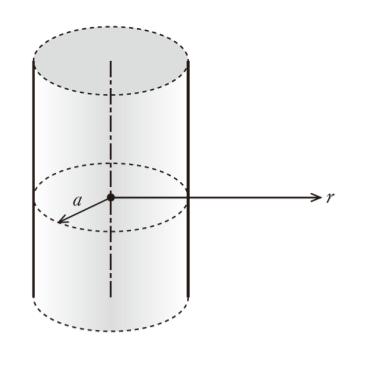
図のように、断面の半径 a の無限に長い円柱の内部に正の電荷が一様に分布している。このとき、円柱の中心軸から距離rにおける電界の大きさ E を定性的に表したものとして最も妥当なのはどれか。
解 説
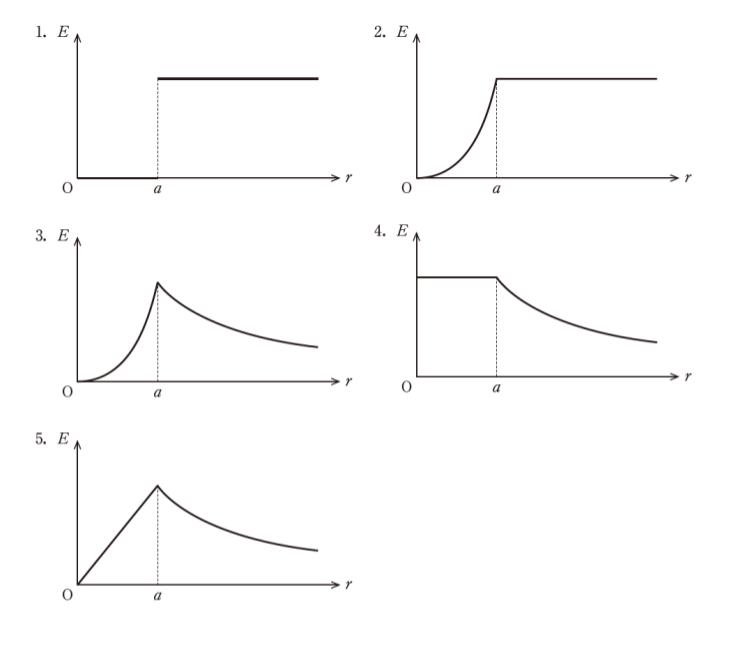
まず、距離 r がとてつもなく大きくなれば、電荷がある場所からどんどん離れていって、E は小さくなるはずです。 E がずっと一定な 選択肢 1,2 は明らかに誤りです。
軸対称性である点に注目し、円柱と同軸の 半径 R, 長さ l の円筒状閉曲面 S を考えます。R < a として閉曲面を取ります。
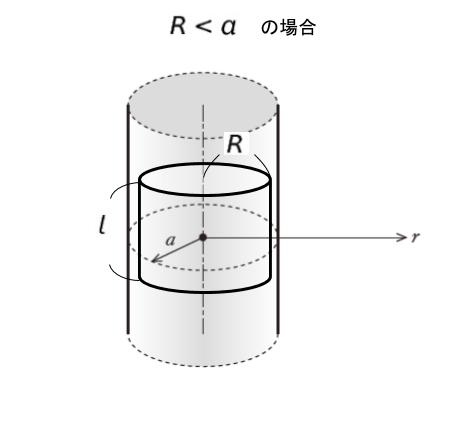
ガウスの法則より、∫E(r)・n(r)dS = 1/ε0 × (閉曲面内の全電荷)です。
上面と下面そして側面という3つの部分に閉曲面を分割して考えます。3つの部分に分けることで、左辺をさらに上面、下面、側面に分割して計算する、ということです。E(r) の方向について、「軸に垂直」です。
以下、「E(r)の方向が、軸に垂直」という点について補足です。
本問の系の対称性から、作られる電場も軸対称(軸から左側、右側に同じ長さ離れたら、電場の大きさ同じはず)かつ、無限に長いから上下ひっくり返しても同じ大きさのはずです。このような対称性を満たすためには、電場の方向は中心軸に対して垂直と考えられます。(なんとなくでいきなり分かる人も多いのかもしれません。)
すると、面に対する単位法線ベクトル n(r) と、E(r) の方向が、上面、下面については垂直になるため、内積 0 です。従って、ガウスの法則の左辺部分は、側面部分のみについて考えればよいとわかります。上面についての図が以下になります。
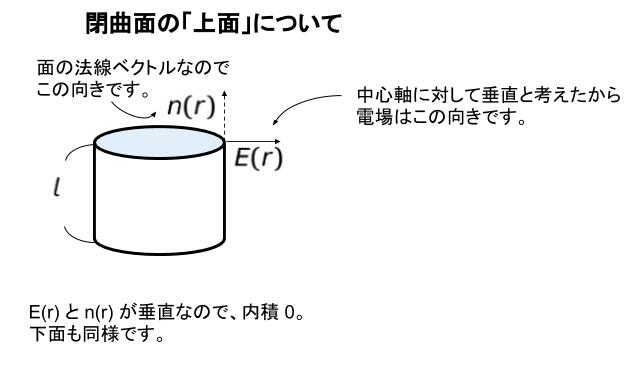
側面部分について、E (r) と n(r) の方向は一致します。従って、内積はそのまま |E(r)| となります。後は ∫ dS ですが、これは半径 R,高さ l の円柱の側面積 です。つまり 2πRl です。
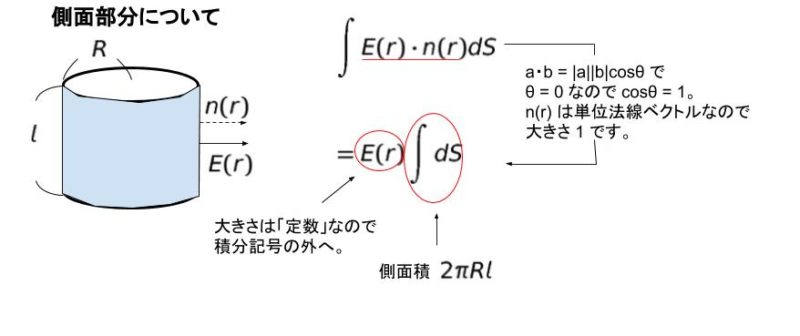
以上より、ガウスの法則の左辺が計算できたことになり、2πRl E(r) が左辺です。
右辺は 1/ε0 × (閉曲面中の電荷の合計)です。円柱の体積は πR2l です。電荷密度が ρ0 なので、電荷の合計は πR2l ρ0 とわかります。 右辺は πR2l ρ0 / ε0 です。
従って、2πRl E(r) = πR2l ρ0/ ε0です。E(r) について解けば E(r) = (ρ0/2ε0)R です。ρ0、ε0 は定数なので、これはE(r) = 1/2 R のような式です。つまり R に比例です。グラフにすれば右上がりの「直線」となります。
以上より、正解は 5 です。

コメント