公務員試験 H24年 国家専門職(教養) No.18解説

　問 題　　　　　

図のように点Ｏを中心とする半径 r の円に、長方形ABCD が内接し長方形ABCD の各辺の長さを直径とした半円を長方形の外側に描いたとき斜線の部分の全面積と長方形ABCD の面積との比はいくらか。

• 斜線部分の全面積：長方形ABCD の面積

1. 1 ： 1
2. √ 3 ： 2
3. 2√ 2 ： 3
4. π ： 3
5. π ： 4

 

 

 

 

 

　解 説　　　　　

公務員試験の戦略

1. 具体的簡単な数で考える
2. 都合よい特殊な状況を考えて簡単にならないかを常に考える

を用いるとこの問はかなり考えやすくなります。

r がなんであれ、長方形がどんな形であれ、斜線部分と長方形の面積比が選択肢のどれかのように、ｒが関係ない定数比になるのだから、r = 1、かつ長方形の一種なので正方形として考えます。

下図において、「黒の部分×４」と、「正方形」の面積比を考えればOKです。正方形の一辺の長さは √２となります。したがって、正方形の面積は (√2)² = 2 です。

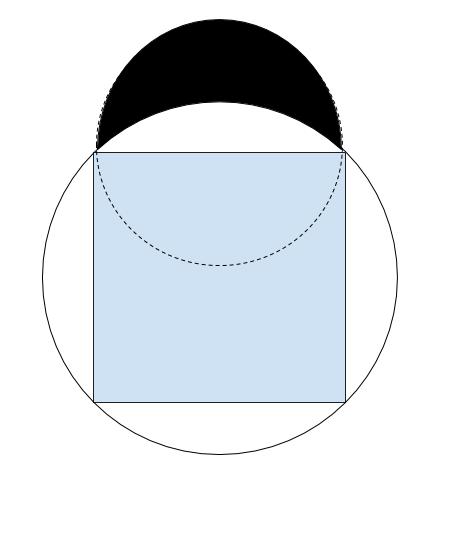
一方黒の部分の面積は、白い部分の面積を半円から削ればOKです。「半径 √2/2 の半円の面積→π/4」です。

白い部分の面積は「扇形ー直角三角形の面積」で求めることができます。中心角が 90°、半径が 1 の扇形の面積は 12π × (90/360) = π/4 です。直角三角形の面積は 1/2 × 1 × 1 = 1/2 です。

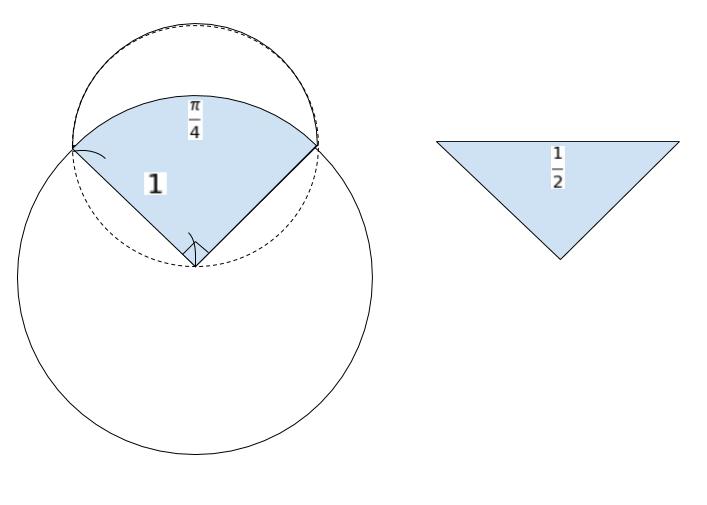
以上より、黒い部分１個の面積は
「π/4」ー「（π/4ー1/2）」 = 1/2 です。したがって、黒の部分４個なら「２」です。正方形の面積も「２」でした。つまり、面積比は １：１です。正解は 1 です。