公務員試験 H24年 国家一般職(化学) No.14解説

　問 題　　　　　

反応速度に関する次の記述の ㋐、㋑ に当てはまるものの組合せとして最も妥当なのはどれか。

「物質 A から物質 B が生成する反応は次のように進行する。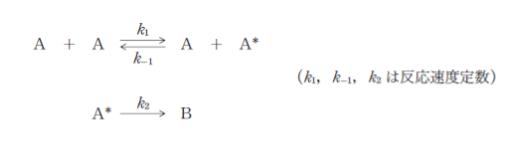

ここで A* は、A から生じる活性な中間体である。A* について定常状態近似が適用できるとすると、B の生成速度 r は r = ㋐と表すことができる。ここで [A] は A の濃度である。k_-1[A] ㋑ k₂ のとき、r は [A] の一次式で表すことができる。」

 

 

 

 

 

　解 説　　　　　

「A*について定常状態近似ができる」という記述があるので、A* の生成速度を式から立ててみます。A→B で反応速度 k ならば B の生成速度は k[A] と表されます。従って、A＋A→A* に注目すれば k₁[A]² ・・・（１）です。一方、逆反応　A＋A*　→　A＋Aで A* は減ります。よって、k_-1[A][A]* ・・・（２）で減ります。さらに、A*→B　の反応でも減るので k₂[A]* ・・・（３）で減ります。
 
（１）～（３）をまとめれば、A* の反応速度は k₁[A]² ー k_-1[A][A]*ーk₂[A]* となります。定常状態である　というのは「変化してない状態」ということです。よって、反応速度の合計が０と考えられます。k₁[A]² ー k_-1[A][A]*ーk₂[A]* = 0 ・・・（４）と表せます。
 
B の生成速度は、k₂[A]* です。選択肢を見ると [A]* を使わずに表せばいいと考えられるため（４）の式を [A]* = ・・・に直して代入してみます。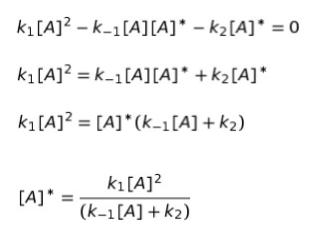

従って、B の生成速度 k₂[A]* は、k₁k₂[A]²/(k_-1[A]+k₂) と表すことができます。正解は 4 or 5です。

k₂ が無視できるくらい小さければ、B の生成速度は k₁k₂[A]²/(k_-1[A]) となり、[A]を約分して [A] の一次式として表すことができます。よって ㋑ は　＞＞　です。

以上より、正解は 4 です。