問 題
△ABC の辺 AB,BC,CA 上にそれぞれ点 P,Q,R をとる。AP:PB = 2:3、BQ:QC = 3:4、CR:RA = 4:5 であるとき、△APQ と △ARQ の面積の比はいくらか。
△APQ:△ARQ
- 1 : 2
- 3 : 5
- 12 : 25
- 21 : 50
- 27 : 50
正解 (5)
解 説
問題文の通り図を書くと、以下のようになります。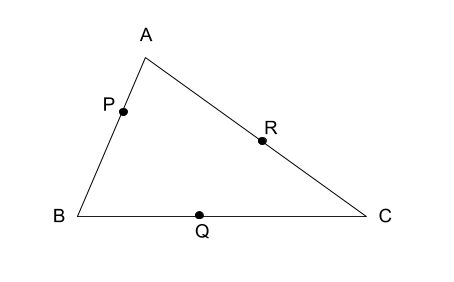
三角形の面積比に関する公式が以下になります。
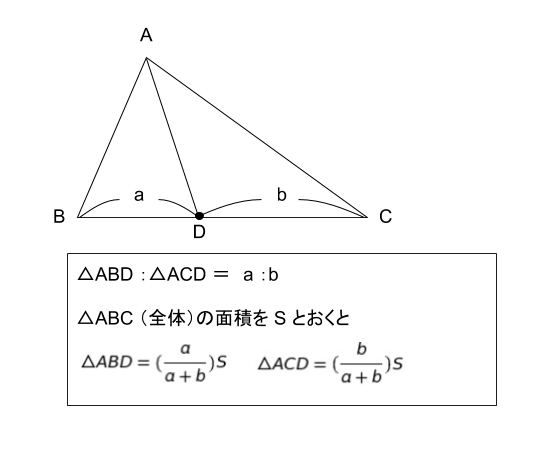
これは基本的知識です。「高さが共通なので、底辺の長さの比がそのまま面積比」ということです。
△ABC の面積を S とおくと、BQ:QC = 3:4より、△ABQ の面積が 3S/7 です。次に、問われている三角形の1つである △APQ に注目します。面積比の公式より△APQ は 2/5 × △ABQ となります。さきほど △ABQ は、3S/7 と出しています。代入すれば
△APQ = 2/5 × 3S/7 = 6S/35 と表すことができます。
同様に、△ACQ の面積は 4S/7 です。△ARQ の面積は、5/9 × △ACQ です。従って △ARQ = 5/9 × 4S/7 = 20S/63 となります。
以上より
△APQ:△ARQ = 6S/35 :20S/63 です。両辺の分母の最小公倍数である 315 をかければ、54S:100S = 27:50 です。
従って、正解は 5 です。

コメント