問 題
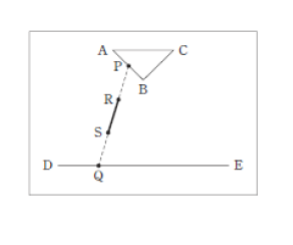
図のように、点Pが三角形ABC の辺上を、点Qが線分DE 上を自由に動くとき、点Pと点Qを結んだ線分を三等分する二つの点をそれぞれR,Sとする。点Rと点Sを結んだ線分RS が動きうる範囲を示したものとして、最も妥当なのはどれか。
なお辺AB と辺BC の長さは等しく、また点Bは、点Aと点Eを結んだ直線と、点Cと点Dを結んだ直線の交点の位置にある。
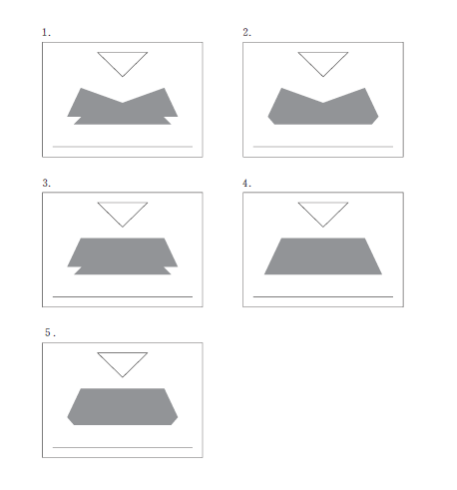
正解 (5)
解 説
動点の問題では、2箇所同時に動いたら訳がわからないので、1箇所固定が定石です。また線分の移動は端点に注目することでわかりやすくなります。
さらに、軌跡の問題なので、選択肢の中でも特徴的な1点に注目することで選択肢の消去法で正解を絞るのが基本となります。
以上をふまえ、まずは「点Qを、ちょうど点D の所に固定」し、「点Pを三角形 ABC に沿ってA→Bに移動させた場合」における RS に注目します。すると、以下の図のようになります。
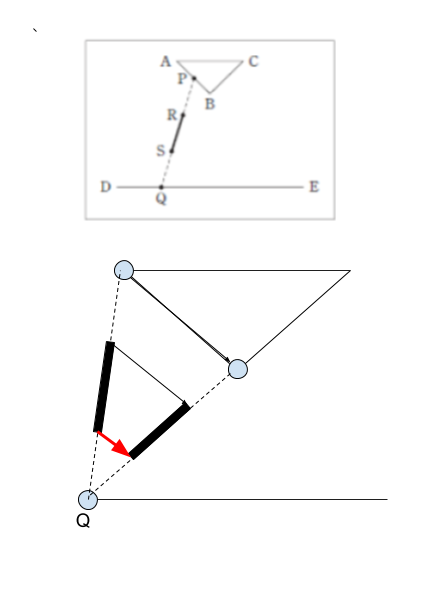
赤矢印で強調した部分に注目すれば、選択肢 1,3,4 は消去されます。左下隅部分が、ABと平行に右下方向になっていないからです。正解は 2 or 5 です。
次に、選択肢 2, 5 を比較すれば、上端が右下がりかまっすぐかの違いに注目すればよいと考えられます。
そこで、点PをA→Cに移動させてみれば、下図のようになります。
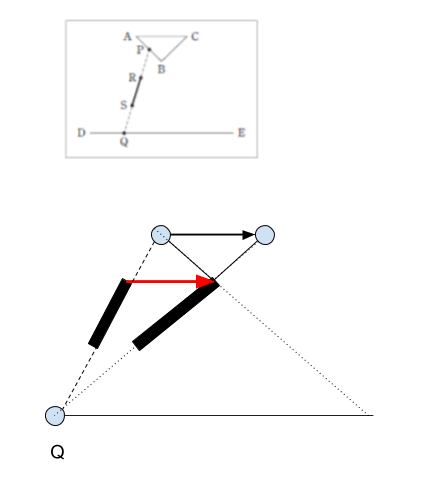
上端はまっすぐでOKです。
従って、選択肢 2 は明らかに誤りです。以上より、正解は 5 です。

コメント