公務員試験 H24年 国家一般職(土木) No.33解説

　問 題　　　　　

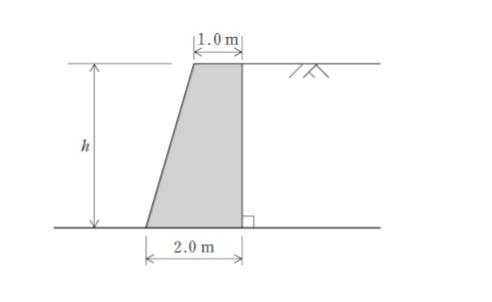
図のような高さ h の擁壁がある。この擁壁の滑動に対する安全率として1.5 以上を確保する場合にh がとりうる最大の値はおよそいくらか。

ただし、土の内部摩擦角を Φ = 30°、土の単位体積重量を 18kN/m³、擁壁の単位体積重量を 24kN/m³ とし、擁壁と基礎地盤の摩擦係数を 0.5 とする。

また、擁壁と背面土の摩擦は考慮しない。土の粘着力は 0 とする。

1. 3.5m
2. 4.0m
3. 4.5m
4. 5.0m
5. 5.5m

 

 

 

 

 

　解 説　　　　　

背面土の土圧を求めます。擁壁が滑動してしまう時の土圧は「主働」土圧です。内部摩擦角がΦ = 30°なので受動土圧係数は tan²(45° – Φ/2) = tan²30° = 1/3。底部の土圧は 18 × h × 1/3 = 6h。

• ※水圧ではなく土圧なので
• ※水平方向の力が弱い。
• ※そのため、係数をかけて求めている。

三角形分布を考えて、全土圧が 6h × h × 1/2 = 3h² 。安全率が 1.5 なので、1.5倍すると4.5h²。これが擁壁による摩擦力よりも大きくなっちゃったら滑ってしまう。

一方、擁壁による摩擦力は台形の面積が 1/2 (1+2)×h = 3/2 h で単位体積重量が 24 なので 24 × 3/2 h = 36h。摩擦係数が0.5なので 36h × 0.5 = 18h です。

4.5h² = 18h となるのがh=4 の時です。つまりh がとりうる最大の値が4です。　

従って、正解は 2 です。