問 題
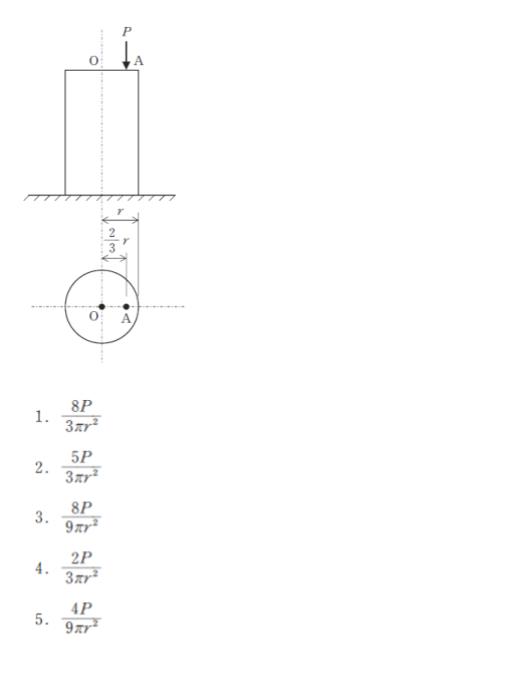
図のように半径 r の円を断面にもち床に固定されている短柱の図心 O から2/3 r 離れた点 A に集中荷重 P を作用させた。
この短柱の底面に生じる引張応力度の最大値として最も妥当なのはどれか。
ただし、短柱の自重は無視する。また、半径 r の円の図心を通る軸に関する断面二次モーメントはπr4/4 である。
正解 (2)
解 説
重心位置に外力 P ならば σc = ーP/A です。
偏心荷重の場合
それに加えて曲げ応力が加わります。曲げ応力は、±M/I × y です。引張側の最大応力はy = r の時、M/I × r です。
M は力×距離なのでP × 2/3 r です。
本問ではA = πr2 です。これらを代入すれば、ーP/A + M/I y は

です。
以上より、正解は 2 です。

コメント