公務員試験 H24年 国家一般職(土木) No.12解説

　問 題　　　　　

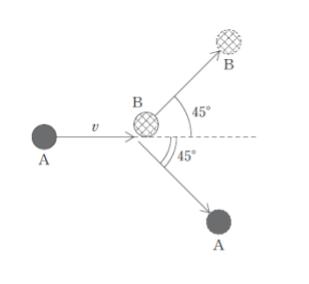
図のように、滑らかな水平面上において、速さ v で運動している質量 m の小球 A を静止している質量 M の小球 B に衝突させたところ 、A は衝突前の運動方向から右へ 45°の向きに B は左に 45° の向きに進んだ。

衝突後の A、B の速さの組み合わせとして最も妥当なのはどれか。

 

 

 

 

 

　解 説　　　　　

衝突と来たら「運動量保存則」を考えます。運動量とは、質量×速さです。衝突の前後で、運動量は保存されます。

衝突前は A の運動量 mv のみです。衝突後ですが A 及び B が斜めに動いているためまず、速度を縦方向と横方向に分けて考えます。

衝突後の A の速度を v_A、B の速度を v_B とおきます。速度を縦、横方向に分解すると 45°の向きに進んでいるのでそれぞれ 1/√2 倍になります。以下の図のように表せます。

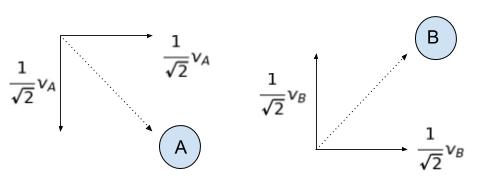
衝突前と衝突後で運動量は保存されるのだから

１：横方向に注目
mv = m(1/√2 v_A) + M(1/√2 v_B) ・・・（１）

２：縦方向に注目
m(1/√2 v_A)=M(1/√2 v_B) ・・・（２）となります。

まず、v_A を求めるために（２）を（１）に代入すれば
mv = m(1/√2 vA) + m(1/√2 v_A) です。両辺を m で割って、同類項を整理すれば
v = 2/√2 v_A です。v_A について解けば v_A = √2/2 v　となります。

よって正解は 1 です。

V_Bについては、求める必要はありませんが求め方は v_Aと同様です。（２）を（１）に代入して
mv = M(1/√2 v_B) + M(1/√2 v_B) より
v_B = m/M √2/2 v となります。