公務員試験 H24年 国家一般職(土木) No.8解説

　問 題　　　　　

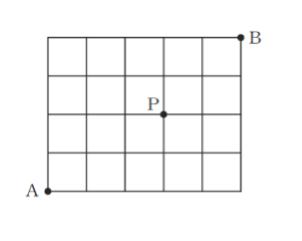
図のように、道路が碁盤の目のようになった街がある。地点 A から地点 B まで行く最短の道順のうち地点 P を通らないものは全部で何通りあるか。

1. 20 通り
2. 33 通り
3. 40 通り
4. 60 通り
5. 66 通り

　解 説　　　　　

『A→Bの最短経路』
A→Bの最短経路は「→→→→→↑↑↑↑」の並びを考えればよいです。矢印の数は全部で 9 本です。その中で同じ矢印が 5本と、4本あるので、並びは 9!/5!4! となります。計算すると、126 通りです。この中でA→P→Bとなるものを除けば答えがわかります。

『A→P　P→Bの最短経路』
A→Pの最短経路は「→→→↑↑」なので、並びの通りは 5!/3!2! です。計算すると、10 通りです。
P→Bの最短経路は「→→↑↑」です。 4!/2!2! を計算すると 6 通りです。

以上より、A→P→Bの経路は 10 × 6 = 60 通りです。

従って、求める経路の数は、126-60 = 66 通りとなります。

正解は 5 です。