問 題
所定の定義域において非負の関数 f(x) について、この定義域における積分値を近似計算するためにこの定義域を単位区間に分割しそれぞれの単位区間の面積の総和を求めることを考える。単位区間の面積を求めるために① ② ③の方法を考えるとき、記述 アイウ のうち、正しいもののみを全て選び出しているのはどれか。
① 単位区間の左端における f(x) の値を横の長さ単位区間長を縦の長さとする長方形の面積で近似する方法。
② 単位区間の左端における f(x) の値を上底の長さ右端における f(x) の値を下底の長さ単位区間長を高さとする台形の面積で近似する方法。
③ 単位区間の中点における f(x) の値を横の長さ単位区間長を縦の長さとする長方形の面積で近似する方法。
ア f(x) が単調減少する場合、①によって求めた積分値は②によって求めた積分値よりも小さい。
イ f(x) の導関数が定数である場合、②によって求めた積分値と③によって求めた積分値は等しい。
ウ f(x) の導関数が定数である場合、③によって求めた積分値と①によって求めた積分値は等しくなることもある。
1. ア
2. ア、ウ
3. イ
4. イ、ウ
5. ウ
解 説
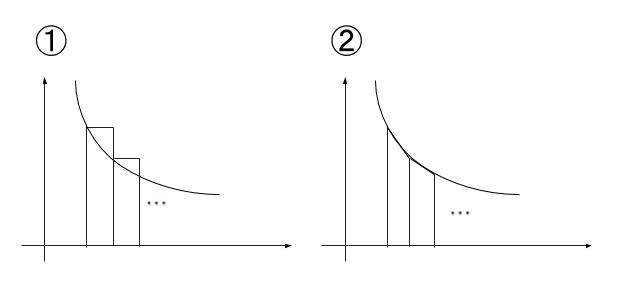
アですが、 f(x) が単調減少する場合、① 及び ② を図示すると以下のようになり、明らかに ① による近似の方が面積が「大きい」です。よって、記述アは誤りです。
イ、ウ ですが、f(x) の導関数が定数とあるので、f(x) は直線です。
イについて、②、③を図示すると以下のようになるため、積分値は等しいと考えられます。
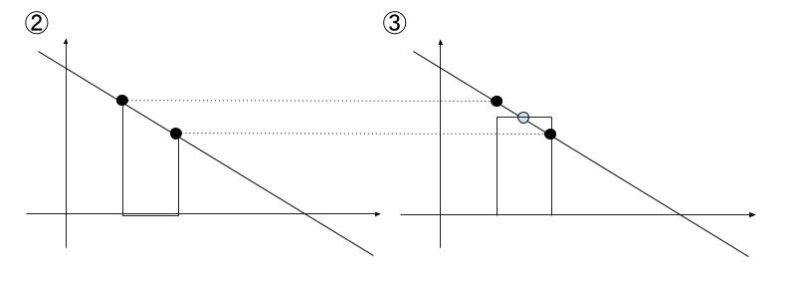
ウについて、導関数が定数ということは、f’(x) = 0 となる、f(x) = 3 のような、x 軸 と平行な場合もありえます。そうであれば、①~③ のどの方法だろうと積分値は同じです。
以上より、正解は 4 です。

コメント