問 題
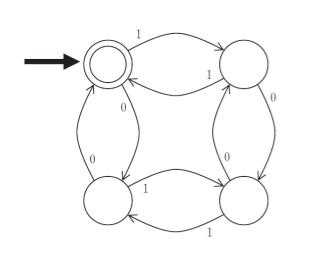
図は入力記号の集合が {0, 1} であり、四つの内部状態をもつ有限オートマトンの状態遷移図である。この有限オートマトンで受理される入力記号列に関する記述として最も妥当なのはどれか。ただし図中の太い矢印が指示する状態は初期状態を二重丸で表された状態は受理状態をそれぞれ表す。
1. 1の個数が偶数、0の個数が奇数である。
2. 1の個数が奇数、0の個数が偶数である。
3. 1の個数と0の個数が、双方とも奇数である。
4. 1の個数と0の個数が、双方とも偶数である。
5. 1の個数と0の個数の和が、奇数である。
4つの状態をそれぞれ「左上」、「右上」、「左下」、「右下」と名付けます。
選択肢 1 の例として、110 を考えます。
最初の 1 で、状態が 右上へいきます。次の 1 で、状態が左上です。最後の 0 で状態が 左下です。二重丸の受理状態の所にいないので、だめです。よって、選択肢 1 は誤りです。
同様に、選択肢 2 の例として 100 を考えると
「右上」→「右下」→「右上」なのでだめです。よって、選択肢 2 は誤りです。
選択肢 3 の例として
10 を考えると、「右上」→「右下」なのでだめです。よって、選択肢 3 は誤りです。
選択肢 4 の例として
1100 を考えると、「右上」→「左上」→「左下」→「左上」なのでOKです。
選択肢 5 の例としては
100 があります。これはすでに選択肢 2 で検討済で、だめです。よって、選択肢 5 は誤りです。
以上より、正解は 4 です。

コメント