問 題
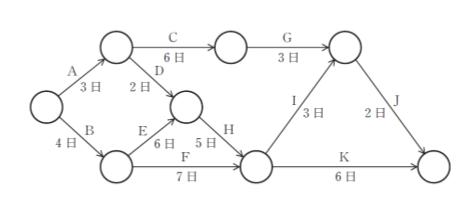
図のアローダイアグラムに関する次の記述の空欄に当てはまる作業名として、最も妥当なのは以下のうちではどれか。
なお図中の ○ は作業の開始及び終了を示す結合点であり矢印の上に作業名下に各作業の所要日数が示してある。また複数の作業に後続する作業は先行する作業が全て終了しなければ開始できない。例えば作業 H は作業 D 及び作業 E が終了してから開始される。作業 □ を1日短縮できれば、全体の作業も1日短縮できる。」
1. A
2. D
3. E
4. F
5. J
正解 (3)
解 説
アローダイアグラム、別名 PERT 図が出てきたら「最速時間」と「最遅時間」をそれぞれの段階に対して求める→余裕時間(最遅ー最速)が0の所をつなぐ→クリティカルパスが見つかる という流れが定石です。
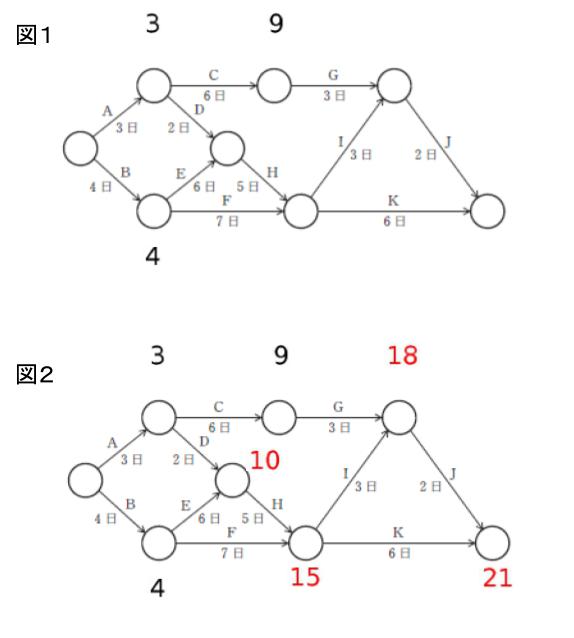
「最速時間」は原則として、左から右に向かって時間を足していけばOKです。この際、ある点に向かう経路が複数ある時、「遅い方の時間」を書き込むのが注意点です。まず、1通りしか行き方がない点までの最速時間を黒数字で書き込んだのが下図1です。複数行き方がある点で、一番遅い時間を赤字で加えたのが下図2です。
最遅時間は、右からかかる時間を引いていけばOKです。最「速」時間の下に、最「遅」時間を書き込んだものが下図です。◯で囲んだ場所が余裕時間が 0 の点です。
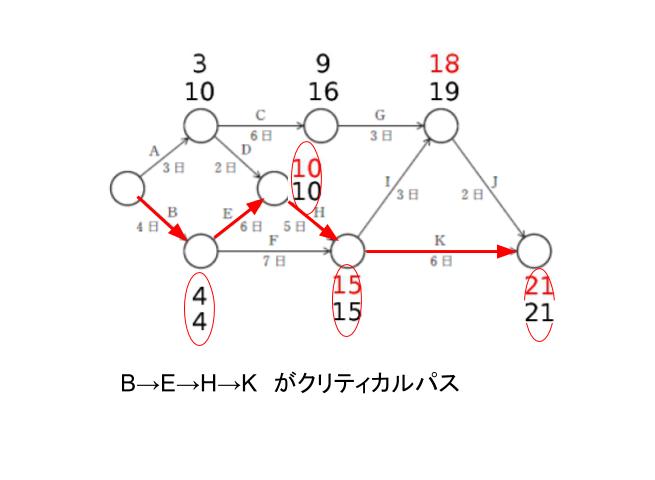
従って、選択肢の中では、作業 E を 1 日短縮できれば、クリティカルパスの時間を 1 日短縮なので、全体の作業も1日短縮できます。
以上より、正解は 3 です。

コメント