問 題
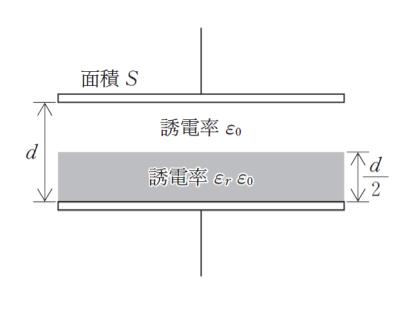
真空中に極板間隔 d, 極板面積 S, 静電容量 C の平行平板コンデンサがある。このコンデンサの極板間に図のように厚さ d/2、面積 S、比誘電率 εr の誘電体を挿入したときの静電容量を C′ とするとき,、C’/C として最も妥当なのはどれか。ただし真空の誘電率を ε0 とする。
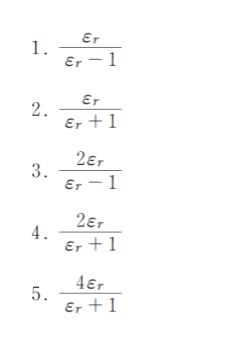
正解 (4)
解 説
コンデンサなので、Q=CV、C = εS/d ※ ε = 1/4πk を思い出します。
また、誘電体の挿入が行われたら、分解して「直列の 2 つのコンデンサ」と考えれば OK です。2つのコンデンサがあって、静電容量がそれぞれ C1,C2 なら、合成すると C1・C2/(C1+C2) です。
まず以下のように、誘電体入りのコンデンサを「2つの直列のコンデンサ」とみなします。
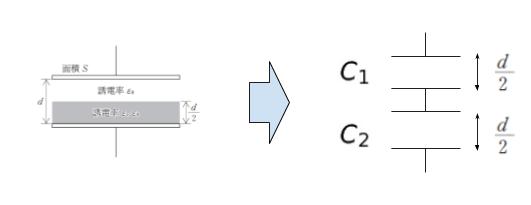
公式より
C1 = εS/(d/2) = 2εS/d、C2 = εrεS/(d/2) = 2εrεS/d なので、合成の公式から
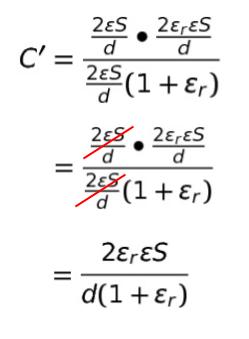
C’/C = C’×1/C = C’ × d/εS なので、残るのは 2εr/(1+εr) です。
以上より、正解は 4 です。

コメント