問 題
長さ240m の列車Aと長さ120m の列車Bがトンネルの両側から同時に入った。列車Aの最前部がトンネルに入ってから最後部がトンネルに入るまでに10秒かかった。
両列車がトンネル内ですれ違い始めてからすれ違い終わるまでに9秒かかりその後列車Aは15秒後に列車Bは45秒後にそれぞれ最前部がトンネルの出口に到達した。
このときトンネルの長さは何m か。ただし両列車の速さはそれぞれ一定であるものとする。
- 1,280m
- 1,360m
- 1,440m
- 1,520m
- 1,600m
解 説
「長さのある列車」では「一点に注目して移動距離を考える」のがポイントです。
列車 A の先っぽ (赤△) に注目します。列車 A は 240m を 10 秒で進んでいるため、1 秒で 24m 進んでいます。
「両列車がすれ違い始めてからすれ違い終わるまで9秒」をイメージするのは少しむずかしいポイントです。この場合のコツですが、両方動いて難しいなら、片方を止めて考えるとよいです。
B が止まっている場合を考え、A B がであい、すれ違い終わるまでを考えると、走った距離は A,B の電車の長さの和となります。つまり、本問であれば、360 m です。
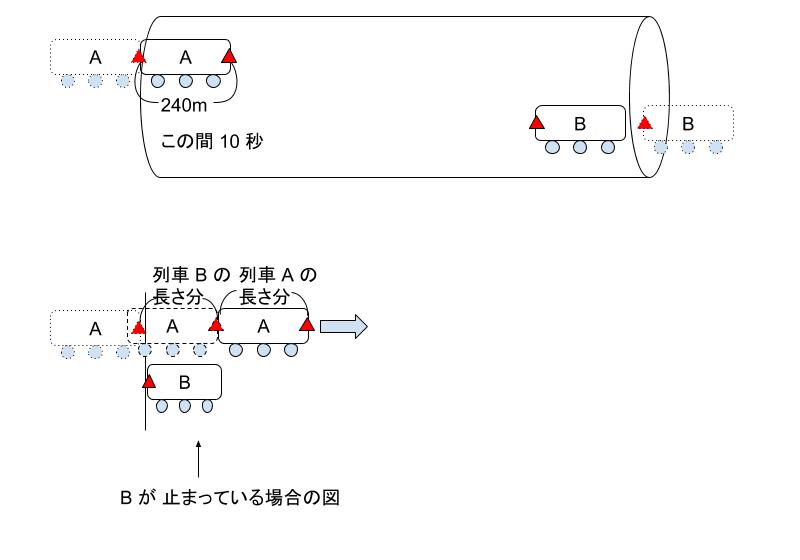
360m を 9 秒なので、1 秒 40m 進んでいます。この 1 秒間に 40m というのは、列車 A 及び 列車 B の秒速の和です。列車 A の秒速は 24m だったので、列車 B は 1秒で 16m 進んでいるとわかります。
列車 A、B が同時にトンネルに入り、速さの比が 24:16=3:2なので、進んだ距離の比も3:2です。そしてトンネルの途中で出会い、9秒ですれ違い、15秒後、列車 A はトンネル出口に到達したことから、比でいう②が24秒です。
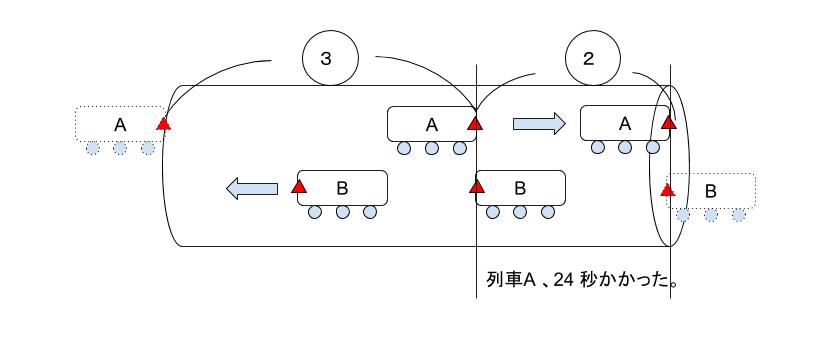
よって、比でいう③が36秒です。合わせて、列車 A は 60秒でトンネル長さ分走っている とわかります。24 × 60 = 1440 m です。正解は 3 です。

コメント