問 題
図のように一辺の長さが1の二つの正方形が重なり合っている。このとき斜線部分の面積はいくらか。
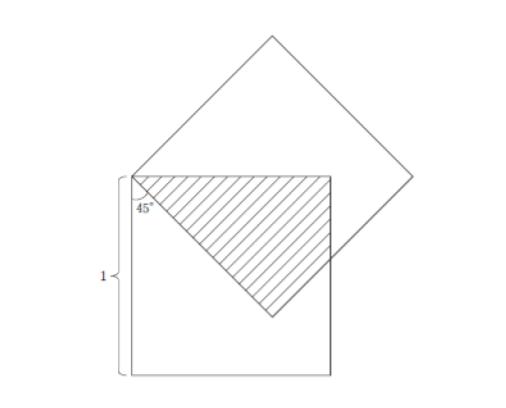
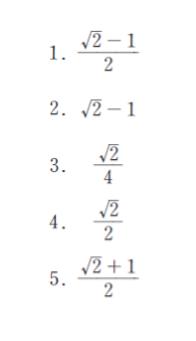
正解 (2)
解 説
前提知識として、直角二等辺三角形の辺の比は1:1:√2です。√2とは、大体 1.4 です。ちょうど 45 °なので、以下のように各辺を延長した補助線を書いてみます。
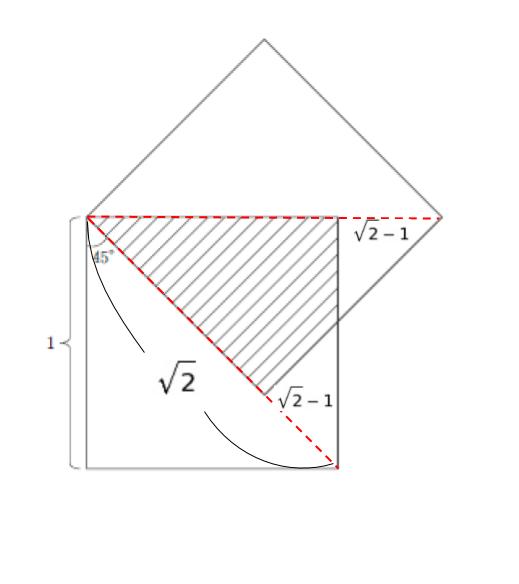
斜辺部の面積は、正方形の半分=面積 1/2 から、底辺、高さが共に「√2 -1」の三角形の面積を引けばよいとわかります。(√2ー1)2 は、3-2√2 なので、白い三角形の部分の面積は(3-2√2 )/2 です。
1/2 ー{(3-2√2 )/2 } = √2-1です。よって、正解は 2 です。
ちなみに、大雑把な面積比較も、ぜひ覚えておいて欲しい解き方です。
本問における面積は、正方形の半分より少し小さいから、0.5 より小さい、大体 0.4 ぐらいと大雑把に面積を評価できます。
そこで、選択肢 に注目すると、√ 2 ≒ 1.4 と読めば、選択肢 1 は 0.2 、選択肢 2 は 0.4 、選択肢 3 は 0.35 、選択肢 4 は 0.7、選択肢 5 は 1.2 です。少なくとも 1,4,5 は明らかに誤りです。
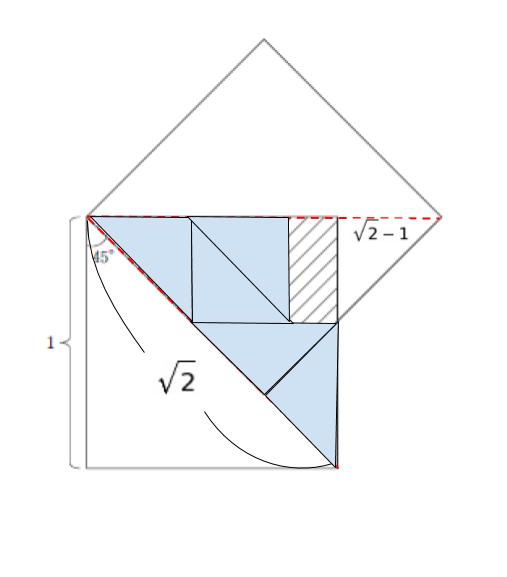
さらに、以下のように評価すると、白い部分 5 個でも 半分には満たないから、白い部分は 0.1 よりは小さい→ 0.5 ー 「0.1 より小さい値」=0.4… となるので、選択肢 3 も誤りと考えることができます。
面積をばしっと求めることができなくても、大雑把な評価で一つでも選択肢を消す という戦術はぜひ頭の片隅に入れておくとよいです。

コメント