問 題
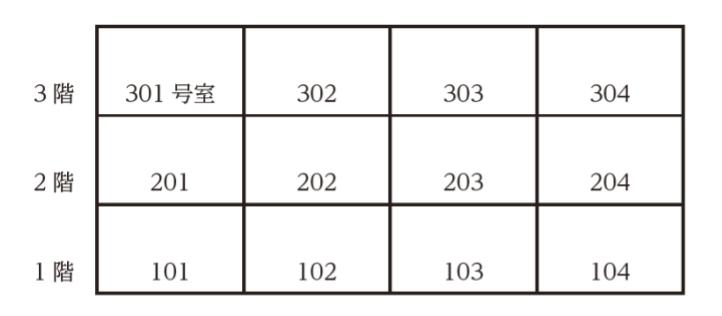
図のような3 階建て12 室のマンションがある。このマンションには,A~Hの8 人がいずれかの部屋に1 人ずつ住んでおり, 4 室は空室である。
A~Hの8 人のうち5 人は音楽家で,それぞれピアノ,ヴァイオリン,フルート,ドラム,クラリネットのいずれか異なる一つの楽器を自室のみで演奏する。
音楽家が楽器を演奏するときには,自室のほか,両隣,一つ真上,一つ真下の部屋にも音が聞こえるが,それ以外の部屋には音が聞こえない。また,音楽家でない3 人は,楽器を演奏しない。
次のことが分かっているとき,確実にいえるのはどれか。
○ 101 号室には音楽家が住んでいる。また,104 号室は空室である。
○ Aは3 階に住んでいる。Aの両隣の部屋のうち,部屋の番号が小さい方は空室で,もう一方は空室ではない。
○ Bは音楽家ではない。Bの部屋では,他の部屋からピアノ,フルート,ヴァイオリン,クラリネットを演奏する音が聞こえる。
○ Cはヴァイオリンを演奏する。
○ Dの部屋では,A,Cが楽器を演奏する音が聞こえる。
○ FとHの部屋は隣どうしである。Fの部屋では,他の部屋からフルート,クラリネットを演奏する音が聞こえる。
○ Gは1 階に住んでいる。Gの部屋では,C,Hが楽器を演奏する音が聞こえる。
1. Aは303 号室に住んでおり,ピアノを演奏する。
2. Fは1 階に住んでおり,ドラムを演奏する。
3. GはHの一つ真下の部屋に住んでおり,楽器を演奏しない。
4. Hは1 階に住んでおり,フルートを演奏する。
5. 3 階には,A~Hのうち3 人が住んでいる。
解 説
A,C,H が複数の条件に出てくるので注目します。D の部屋で A,C が楽器を演奏する音が聞こえて、A が 3F ということなので、C の 階数を仮定して考えてみます。
C 1F とすると、A 3F で、D が 2人の演奏が聞こえることから、C→D→A と縦に住んでいるはずです。104 は空き部屋です。101 号室とすると、「A に両隣がいる」という点に矛盾します。従って、C の候補は 102,103 号室となります。
C 102 号室のパターンを考えると、下図のようになります。
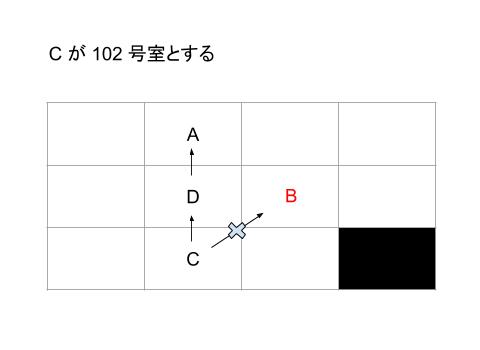
C がヴァイオリン演奏者で、B はヴァイオリンを含む「4人の演奏」が聞こえています。B は 203 号室と確定します。今回のパターンでは、C の 右隣の 103 号室しかヴァイオリンが聞けず、このパターンはありえません。同じ理由で、C 103 号室もありません。
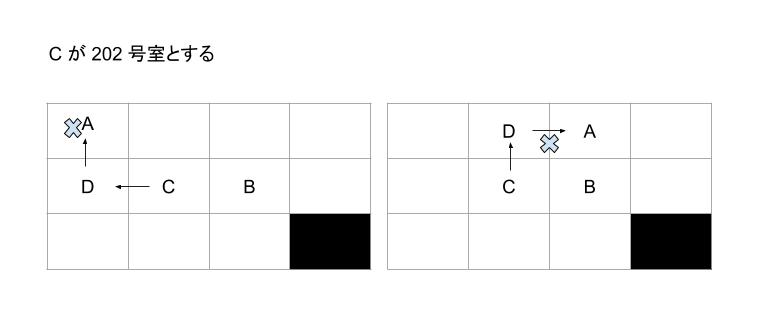
次に C 2F のパターンを考えます。C が 202 号室とします。B が「4人の演奏」が聞けるので、B は 203 号室しかありません。201 をD、301 をA とすると、「A には両隣がいる」という点と矛盾します。また、302 を D にすると、A の「隣の部屋番号が小さい方が空き室」という条件を満たせません。以上より、C 202 は無理です。
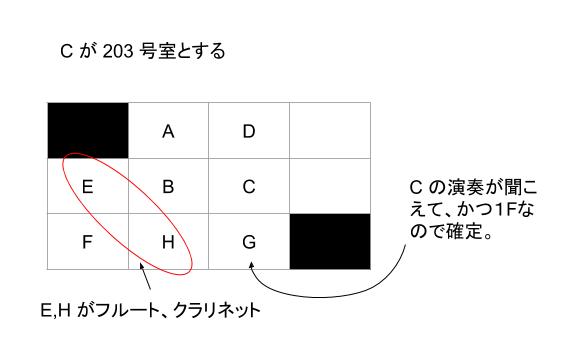
そこで、C 203 号室とします。C の演奏が聞こえて かつ 1F なので G が 103、G は H の演奏が聞こえているから H が 102、F と H が隣合うため、H が 101 号室です。
以下のようなパターンが(やっと!)見つかります。このパターンにおいて、F の部屋ではフルート、クラリネットが聞こえてくるので、F の上が E です。E と H のどちらかがフルート、どちらかがクラリネット奏者です。
すると、選択肢 1,3,5 は明らかに誤りです。さらに、選択肢 4 は確定しません。
以上より、正解は 2 です。
101号室である F が音楽家なので、F は B の周囲4人(A,C,E,H) の演奏する楽器を除外し、残った楽器であるドラム奏者と確定します。

コメント