問 題
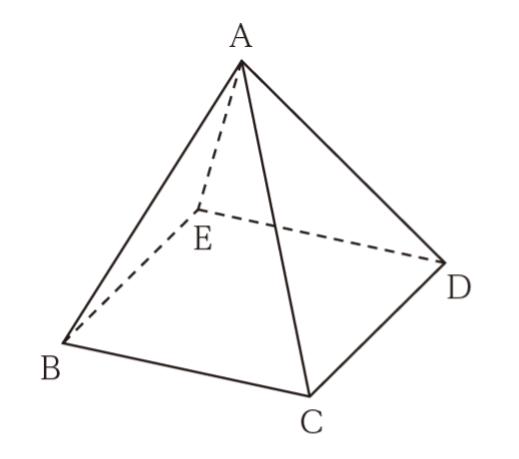
図のような四角錐の頂点 A から出発し、四角錐の辺上を通って頂点を次々に移動する経路を考える。
ある頂点から辺で結ばれた隣の頂点のいずれかへの移動を 1 回の移動とし、1 回の移動では最短経路をとるものとする。このとき、頂点 A から 4 回の移動を終えた時点で頂点 A にいるような移動経路の数は全部でいくつか。
1.8
2.16
3.24
4.32
5.40
解 説
選択肢から、せいぜい 40 通りなので、最悪数え上げようと考えます。A と A 以外の4つの頂点に分けると考えやすいです。
まず、点が1回移動する場合について、以下のように場合分けができます。
1:【A→A以外への移動】
A → A以外 は、100% 移動します。この移動は移動先が B,C,D,E なので「4通り」考えられます。
2:【A以外→Aへの移動】
これは 1 通りです。
3:【A 以外 → A 以外への移動】
これは2通り考えられます。
これをふまえ、4回の移動を、1回めから順に考えてみます。
【1回めの移動】
A→A以外なので4通り考えられます。
【2回めの移動(1)】
A 以外 → A と2回めに移動したとします。すると3回めの移動が、A→A以外と確定します。4回めに A にいるためには、A以外→A→A以外→A と移動しなければならないからです。このパターンは、1×4×1=4通りです。1回めの移動が4通りあったので、全パターンは、4×4=16通りです。
【2回めの移動(2)】
A 以外 → A 以外と2回めに移動したとします。すると、3回めの移動で A に行ってしまうとどうしても4回めの移動で、A以外に行ってしまいます。従ってA以外→A以外→A以外→A と移動しなければなりません。このパターンは、2×2×1=4通りです。1回めの移動が4通りあったので、全パターンは、4×4=16通りです。
以上より、合わせて32通りです。正解は 4 です。
ちなみに、全てのパターンをあげてみると
A→B→A→B→A
A→B→A→C→A
A→B→A→D→A
A→B→A→E→A
A→C→A→B→A
A→C→A→C→A
A→C→A→D→A
A→C→A→E→A
A→D→A→B→A
A→D→A→C→A
A→D→A→D→A
A→D→A→E→A
A→E→A→B→A
A→E→A→C→A
A→E→A→D→A
A→E→A→E→A
A→B→C→B→A
A→B→C→D→A
A→B→E→B→A
A→B→E→D→A
A→C→B→C→A
A→C→B→D→A
A→C→D→C→A
A→C→D→E→A
A→D→C→B→A
A→D→C→D→A
A→D→E→B→A
A→D→E→D→A
A→E→B→C→A
A→E→B→E→A
A→E→D→E→A
A→E→D→C→A です。

コメント