問 題
シュレーディンガー方程式に関する次の記述のア~エに当てはまるものの組合せとして最も妥当なのはどれか。
「量子力学ではシュレーディンガー方程式を解くことによりアを求めることができる。シュレーディンガー方程式は
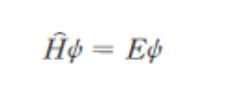
で表される。ここでψは波動関数であり ψ の絶対値の2乗が ア に相当する値となる。また E は イ である。H(上に^) はハミルトニアンと呼ばれる演算子であり
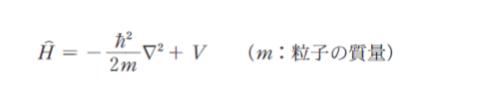
で表される。ハミルトニアンの第1項は ウ に V は エ に対応する。」
| ア | イ | ウ | エ | |
| 1. | 粒子をある位置に見いだす確率 | エネルギー固有値 | 粒子の運動エネルギー | 粒子の位置エネルギー |
| 2. | 粒子をある位置に見いだす確率 | リュードベリ定数 | 粒子の位置エネルギー | 粒子の運動エネルギー |
| 3. | 粒子の運動エネルギー | エネルギー固有値 | 粒子をある位置に見いだす確率 | 粒子の位置エネルギー |
| 4. | 粒子の位置エネルギー | エネルギー固有値 | 粒子の運動エネルギー | 粒子をある位置に見いだす確率 |
| 5. | 粒子の位置エネルギー | リュードベリ定数 | 粒子をある位置に見いだす確率 | 粒子の運動エネルギー |
正解 (1)
解 説
シュレディンガー方程式を解いて波動関数 というものを求めるのですが、波動関数のイメージとしては y = ex・sinx・cosx・・・ みたいな感じの式で係数がすごくごちゃごちゃしているもの です。式なので、グラフを書いて絵として表すことができ、このグラフが表すのが、対象としている波が存在する領域、つまり例えば電子がどこにあるのかを表します。
ア に入るのは「位置エネルギーや運動エネルギーではありません」。従って、アは「粒子をある位置に見いだす確率」です。正解は 1 か 2 です。
次に、リュードベリ定数は普通 R で表され、原子の「スペクトル系列」に関する式に出てくる定数です。シュレディンガー方程式には、出てきません。従って、イ は「エネルギー固有値」です。
以上より、正解は 1 です。ちなみに、ウ、エ も有名な事実ですので、この機会にぜひ覚えておくとよいです。

コメント