問 題
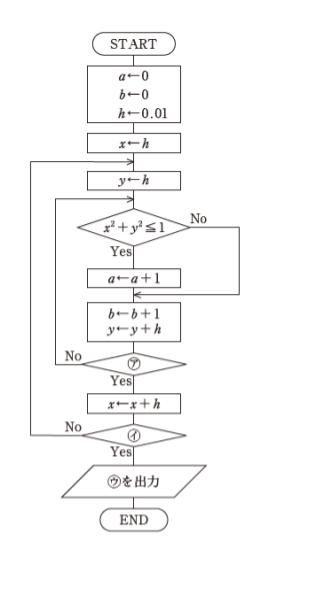
図は、辺の長さ 1 の正方形の面積と、半径 1 で中心角 90° の扇形の面積の比を用いて円周率 π の近似値を求めるためのフローチャートである。図中のア~ウに当てはまるものの組合せとして最も妥当なのはどれか。なお、二つの図形の面積の比は、以下の1~4の考え方を使って求めている。
1 xy 平面を考え、h≦x≦1、h≦y≦1 の区間に刻み幅 h で、合計1/h2 (= 1/h × 1/h) 個の点を打つ。
2 1 のxy 平面の点(0,0),(0,1),(1,0),(1,1) を頂点とする正方形に含まれる点の数を求める。
3 1 のxy 平面の原点に中心を置いて描いた半径 1 の円の x > 0 かつ y > 0 の領域に含まれる点の数を求める。
4 2、3で求めた数の比を、正方形の面積と扇形の面積との比の近似値とする。
ア イ ウ
- y > 1 , x > 1 , 4×a ÷ b
- y > 1 , x > 1 , 4×b ÷ a
- x ≦ 1 , y≦ 1 , 4×a ÷ b
- x ≦ 1 , y≦ 1 , 4×b ÷ a
- y≦ 1 , x ≦ 1 , 4×b ÷ a
解 説
アの所までチャートを読むと以下のようになります。
(a,b,h) = (0,0,0.01)
(a,b,x,y,h) = (0,0,0.01,0.01,0.01)y
(a,b,x,y,h) = (1,1,0.01,0.02,0.01)
問題文より、h は刻み幅とわかっています。また、ここまでのチャートより、a,b は1ずつ増えていくことが読み取れます。ここまででやっていることは以下の図のようにまとめることができます。
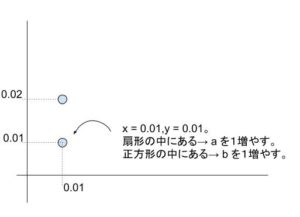
【ア、イについて】
選択肢 より、アに入るのは y>1 か、x ≦ 1 か、y≦1 です。
アの分岐で yes だと、次で x が 0.02 となってしまいます。x = 0.01 のまま、 y がどんどん増えていくことで x = 0.01 上の点を全て考えることができるため、この分岐は、まずは 「no」 でぐるぐるまわると考えられます。アに入るもので、この時点で no になるのは y > 1 という条件のみです。従って、正解は 1 or 2 です。また、イに入るのは x > 1 とわかります。
【ウ について】
a の個数が 扇形に含まれる点の数で、b の個数が 正方形に含まれる点の数です。面積が大きい方により多く点が含まれるはずです。扇形の面積は 半径1の円の 1/4 だから π/4 です。正方形の面積は、1 です。
従って、まず、a : b は π/4 :1 となるはずです。※ π≒3.14 だから、π/4 :1 ≒ 0.7 :1ぐらい。
求めたいのは、π の近似値だったので、選択肢 1 が正解と仮定して 4a÷b を計算してみます。a : b は π/4 :1 → 4a:b = π:1 なので、パラメータ k を用いて 4a = kπ、b = k とおけて、4a ÷ b = kπ ÷ k = π となります。うまくπ になったため、正解と考えられます。
以上より、正解は 1 です。

コメント