2020 (R2) 年 国税専門官 No.62 解説

　問 題　　　　　

0 ≦ x ≦ π の範囲で、cos (πcosx) = 1/2 を満たす実数 x はいくつあるか。

1． 1 個
2． 2 個
3． 3 個
4． 4 個
5． 5 個

 

 

 

 

 

　解 説　　　　　

π cosx を θ とおきます。何かを別の文字で置いたらすぐ範囲を確認します。
0 ≦ x ≦ π なので、-1 ≦ cosx ≦ 1 です。従って、－π ≦ θ ≦ π です。 

cos θ = 1/2 → θ = ± π/3 です。
θ を元に戻すと π cosx = ± π/3 です。

つまり、cos x  = ± 1/3 を満たすような x が
0 ≦ x ≦ π でいくつあるか という問に帰着します。

単位円を考えれば
具体的な x の値はわかりませんが、x が 2 つあることはわかります。

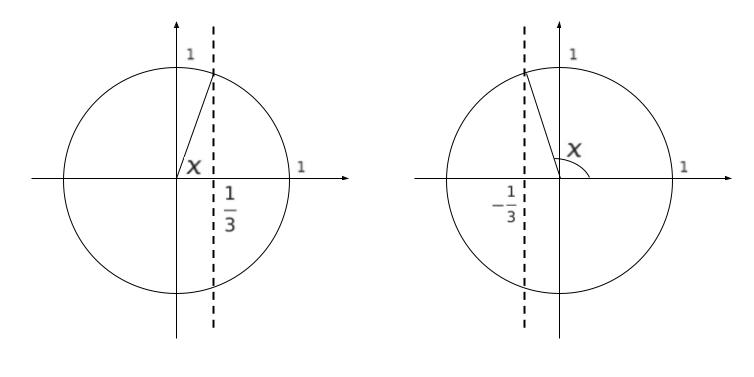
以上より、正解は 2 です。