問 題
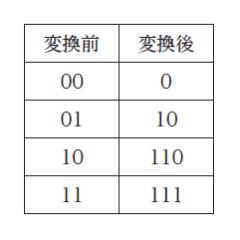
0,1 の出現確率がそれぞれ 90 %、10 % である長さ n のビット列がある。ビット列の先頭から 2 ビットずつに区切った後、表に示す変換を行う。変換後のビット列の長さの期待値を n で割った値はおよそいくらか。ただし、n は正の偶数とする。
1. 0.58
2. 0.65
3. 0.75
4. 0.81
5. 1.1
解 説
具体的ビット列で考えることから始めるとよいと思われます。
例えば 『0001』 というビット列を考えます。
0001 を先頭から 2 ビットずつ区切れば「00」「01」となります。表に従って変換すれば 00 → 0、01 → 10 となるので、変換後のビット列は 010 です。変換後のビット列の長さは 3 なので、元のビット列の長さ 4 で割ると 3/4 となります。
2 ビットずつ区切った時に「00」 なのか 「01」 なのか 「10」 なのか 「11」 なのかというのは、確率で表すことができます。
00 となる確率は 0.9 × 0.9 = 0.81 です。
この確率で 変換後 1 文字になります。
01 となる確率は 0.9 × 0.1 = 0.09 です。
この確率で 変換後 2 文字になります。
10 となる確率は 0.1 × 0.9 = 0.09 です。
この確率で 変換後 3 文字になります。
11 となる確率は 0.1 × 0.1 = 0.01 です。
この確率で 変換後 3 文字になります。
従って
2 ビットずつの各区切りについて、変換後のビット列長さの期待値は
(0.81 × 1) + (0.09 × 2) + (0.09 × 3) + (0.01 × 3) = 1.29 文字です。
2 文字 → 1.29 文字になる変換とわかりました。
1.29 ÷ 2 ≒ 0.65 です。
以上より、正解は 2 です。

コメント