公務員試験 2022年国家一般職(土木) No.23 解説

　問題　　　　　

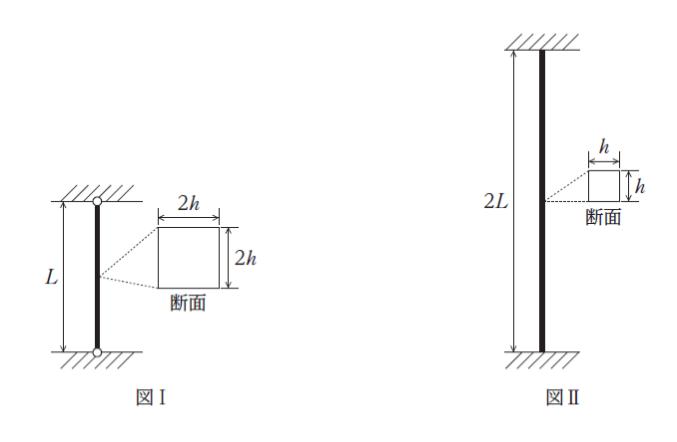
図Ⅰと図Ⅱのような支持条件、長さ、断面が異なる長柱の座屈荷重をそれぞれ P_Ⅰ、P_Ⅱとするとき、これらの大きさの組合せとして最も妥当なのはどれか。ただし、図Ⅰと図Ⅱの長柱の Young 係数 E は同じで、断面は長さ方向に一様とする。

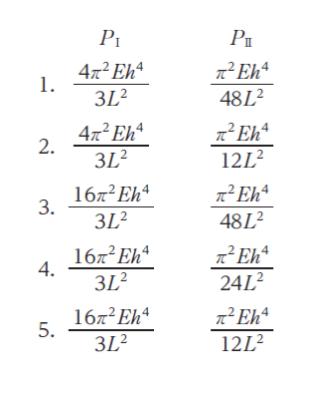
正解 (2)

　解説　　　　　

【座屈の基礎知識】
座屈は、柱に対して荷重をかけた際、急激に折れ曲がる現象です。座屈では、オイラーの座屈荷重 P＝π²EI/l_k² をまず思い出します。

座屈長さ l_k については、長さ l(エル) に対して『両端ピン　l、一端ピン0.7l、両端固定（※水平移動拘束）0.5l 、一端が自由 2l』と補正します。分子の I (アイ) は断面 2 次モーメントです。

図Ⅰでは両端ピンなので、長さ L をそのまま式に代入します。
P_Ⅰ = π²EI/L² です。

断面は正方形 (長方形) なので、断面二次モーメントは bh³/12 です。b = 2h、h = 2h を代入すれば 4h⁴/3 です。

従って
P_Ⅰ= (4/3) × π²Eh⁴/L² です。正解は 1 or 2 です。

図Ⅱでは両端固定なので 0.5 × 2L を l_k に代入します。
P_Ⅱ = π²EI/L² です。

断面二次モーメントは h⁴/12 です。

従って
P_Ⅱ = π²EIh⁴/12L² です。

以上より、正解は 2 です。

コメント