問 題
半径 r、ヤング係数 E、長さ 4r、線膨張係数 (単位温度変化当たりの軸方向のひずみ度) α の円形断面の棒材がある。この棒材の両端を固定壁間に固定して、一様に棒材の温度を ΔT 上昇させたとき、棒材に生じる軸力の大きさはいくらか。ただし、棒材の自重は無視するものとする。
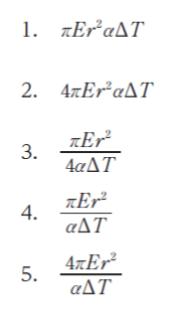
正解 (1)
解 説
「線膨張係数」や温度変化 ΔT が出てきて 「えっ、知らない、ムリ」といいたくなったかもしれませんが、落ち着いて問題文の「単位温度変化当たりの軸方向のひずみ度」に注目すれば「1 ℃ 上がった時にひずみが α」という内容です。
【ひずみに関する基礎知識】
力を加えて、元々 長さ l の物体が Δl 伸びた時、ひずみ ε を Δl/l で表します。この時、E をヤング係数(ヤング率)として、σ = Eε が成立します。σ は軸応力です。軸方向力を P、断面積 A とすると、軸応力 σ は P/A です。
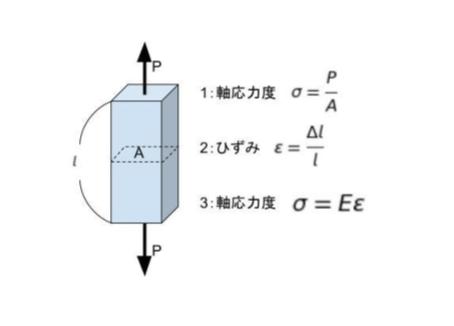
1 ℃上昇した場合を考えます。
σ = P/A = E × α です。A = πr2 なので
P = πr2 × E × α…(1) です。
ΔT 上昇した時は
(1) × ΔT と表されます。
以上より、正解は 1 です。
類題 2020 no24
https://yaku-tik.com/koumuin/2020-doboku-24/

コメント