問 題
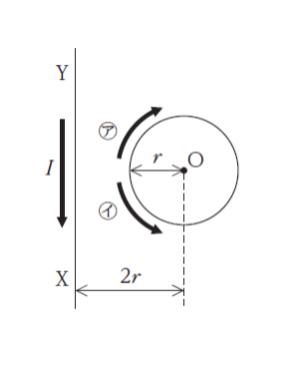
図のように、半径 r の円形導線の中心 O から 2r 離れた位置に十分に長い直線導線 XY があり、XY には Y から X に向けて大きさ I の電流が流れている。ここで円形導線に電流を流すと、O における磁場の強さが 0(ゼロ)になった。
円形導線に流れている電流の向きと大きさの組合せとして最も妥当なのはどれか。ただし、円形導線と直線導線は同一平面上にあるものとする。
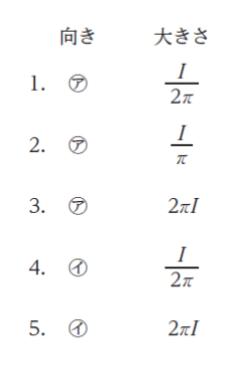
解 説
【直線電流が作る磁場】
直線電流 I が作る磁場の強さ H は、直線から r 離れている場所において H = I/2πr です。これが基礎知識です。ちなみに向きは、右ねじの法則でわかります。右手の親指を電流方向に向けて、手のひらを軽く握った時の、親指以外の4本の指の方向が磁場の向きになります。
【円形電流が作る磁場】
半径 r の円形電流が中心に作る磁場 → H = I /2r が基礎知識です。向きは右ねじの法則でわかります。右手の親指を立てて手のひらを軽く握った時の、親指以外の4本の指の方向を円形電流の流れる向きに合わせた際の、親指の向きが対応します。
直線電流 I により、点 O を「紙面の下 → 上に貫く方向」に、I/2π × (2r) の大きさの磁場…(1) が作られます。
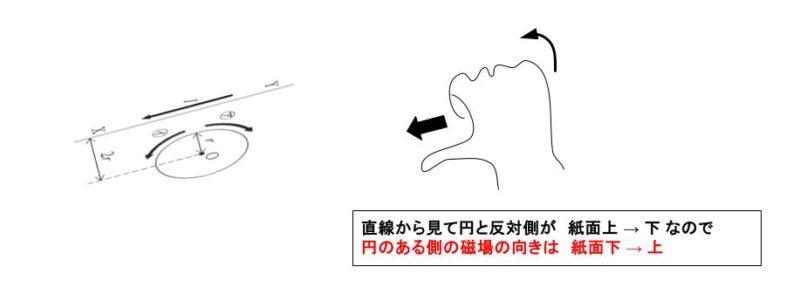
円形電流 により、点 O には I/2r の大きさの磁場が作られます。向きは (1) の磁場と打ち消し合うので「紙面の上 → 下に貫く方向」でなければいけません。従って、右ねじの法則より ㋐ です。
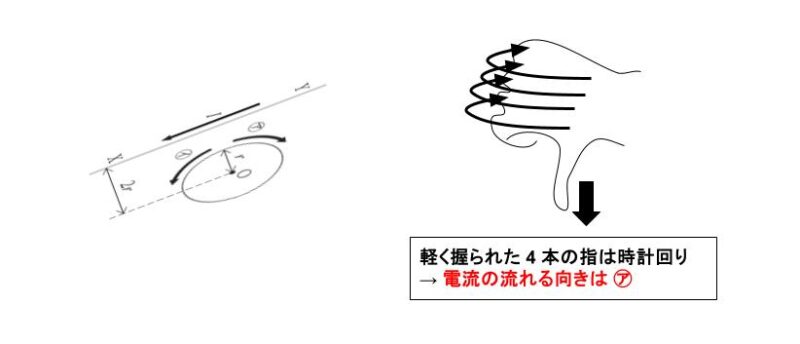
直線電流と円形電流が作る磁場が打ち消し合うので、大きさは等しくなければなりません。円形電流を X とおけば、X/2r = I/4πr です。従って、X = I/2π です。
以上より、正解は 1 です。

コメント