問 題
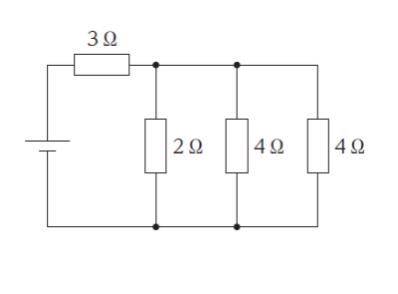
図のような回路において、抵抗値 3 Ω の抵抗で消費される電力を P1 とし、回路全体で消費される電力を P2 とすると、P1/P2 として最も妥当なのはどれか。
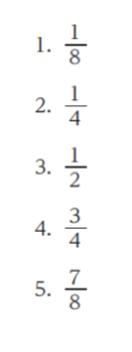
正解 (4)
解 説
図の回路は、直並列回路の一部が更に並列回路になったものです。以下のように書き換えるとわかりやすいと思われます。
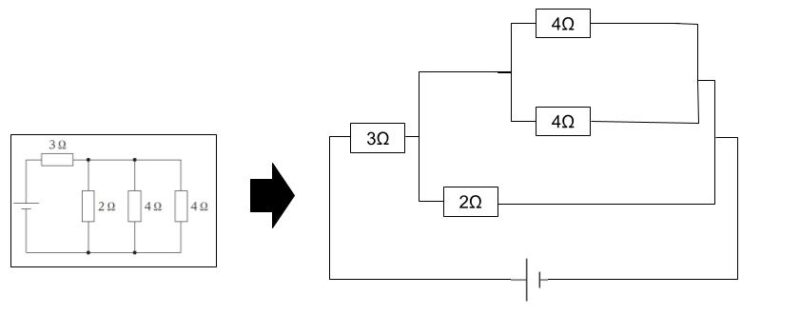
並列抵抗の合成は「分子はかける、分母は足す」です。
・4 Ω と 4 Ω の並列部分を合成すると 4・4/(4+4) = 2 Ω です。
・2 Ω と 2 Ω の並列を合成すれば 2・2/(2+2) = 1 Ω です。
図の回路は結局
3 Ω と 1 Ω の直列とみなせます。合成すれば、全体の抵抗は 3 + 1 = 4 Ω です。
電源の電圧は特に指定がないため、例えば 4 V と設定して考えます。すると、全体を流れる電流はオームの法則 V = RI より I = 1 A となります。回路全体で消費される電力 P2 は P = VI なので 4 × 1 = 4 W です。
3 Ω の抵抗部分は、並列に枝分かれする前なので、流れる電流は 1A です。この部分にかかる電圧は V = RI より 3V です。従って、3 Ω の抵抗部分で消費される電力 P1 は 3 × 1 = 3 W です。
従って、P1/P2 = 3/4 です。
以上より、正解は 4 です。
類題 2022 no19
https://yaku-tik.com/koumuin/2022-doboku-19/

コメント