問 題
軽いばねの一端を天井に固定し、他端に小物体 P を取り付けると、ばねが自然長から 5.0 × 10-2 m 伸びて釣り合った。その後、P を鉛直方向に少しだけ引っ張り静かに放すと、P は鉛直方向に単振動した。この単振動の角振動数として最も妥当なのはどれか。ただし、重力加速度の大きさを 9.8 m/s2 とする。
1. 7.0 rad/s
2. 10 rad/s
3. 14 rad/s
4. 17 rad/s
5. 21 rad/s
正解 (3)
解 説
単振動なので周期の公式を思い出します。ばね振り子なので
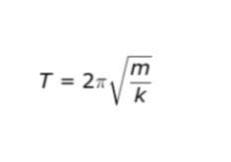
です。
小物体 P の質量を m とおきます。下向き mg の力が作用します。フックの法則 F = kx より、mg = 0.05k です。g = 9.8 を代入して、小数を整数にするために両辺 20 倍すれば 196m = k なので「m/k = 1/196」を得ます。
周期 T = 2π × √1/196 = π/7 です。振動数と周期の関係は f = 1/T です。そして角振動数と周期の関係は f角振動数 = 2π/T です。※1 回振動 = 2π rad です。
求める単振動の角振動数は
2π/T = 14 (rad/s)です。
以上より、正解は 3 です。

コメント