問 題
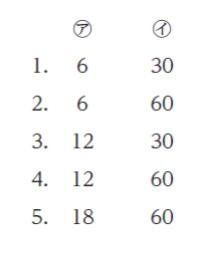
場合の数に関する次の記述の ㋐、㋑ に当てはまるものの組合せとして最も妥当なのはどれか。
「正六面体のサイコロは、一般に、向かい合う面の目の数の和が 7 になるように面を配置するというルールに従っている。このルールの下では、回転させると目の数の並びが同じになるものを一つの種類として数えると、図のようにサイコロの種類は 2 種類となる。
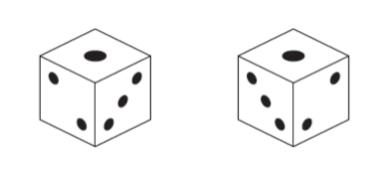
このルールを一部なくし、1 と 6 の面は向かい合う位置に残したまま、2 ~ 5 の面を自由に配置してよいとした場合、上記と同じ方法で数えると、サイコロの種類は ㋐ 種類となる。さらに、このルールを完全になくし、1 ~ 6 の面を自由に配置してよいとした場合、上記と同じ方法で数えると、サイコロの種類は ㋑ 種類となる。」
解 説
㋐ ですが
「1 と 6 の面は向かい合う位置に残したまま」とあるので「上下固定」です。そして 4 面に関して自由に配置していいので「向かい合う面の目の数の和が 7」というルールは無視してよいです。「回転して目の数の並びが同じになるものを一つの種類」とするので「4 つの席の円順列」と読み替えることができます。
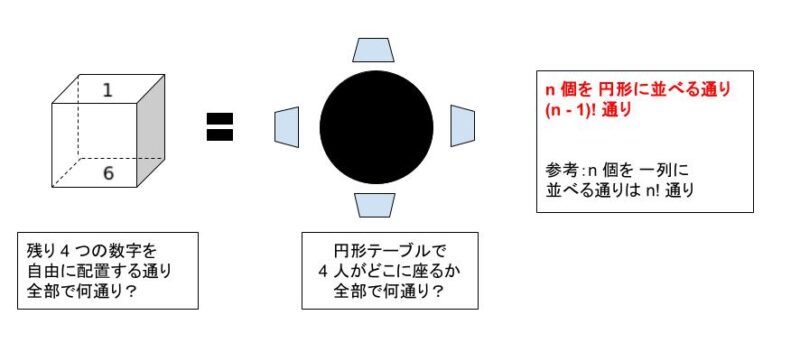
n 個ある場合、円順列の場合の数は「(n – 1)!」です。従って、本問では (4 – 1)! = 6 通りです。㋐ は「6」です。正解は 1 or 2 です。
㋑ ですが
上下固定にも色んな場合が考えられるということになります。上下の固定は 6 個の数値から 2 個を選ぶ場合があるので 6C2 = 15 通りです。すると 15 × 6 = 90 通りあるように思えます。選択肢より多くなってしまいます。
ここで「1 と 6 を対面にしたもの」を考えると、対面になる場合が 3 通りあるため、90 通りの中には 3 通り同じものが含まれています。
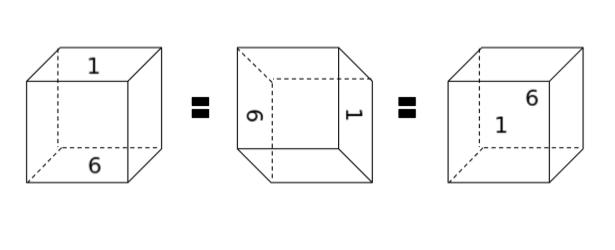
「上下が 1 と 6」だけでなく、上下の固定で選んだ 15 通り全てに関して、3 通りずつが同じ種類になります。従って、求める通りは「90 ÷ 3」= 30 通りです。㋑ は 30 です。
以上より、正解は 1 です。

コメント