公務員試験 2023年 国家一般職(土木) No.5 解説

　問 題　　　　　

関数 y = -4^x+1 + 2^x+2 の最大値はいくらか。

1． 1
2． 2
3． 3
4． 4
5． 5

 

 

 

 

 

　解 説　　　　　

指数方程式として解いたことがあれば、2^x = X とおいて最大値を求めれば OK です。ぱっと見て解き方が浮かばなかった時は、具体的な値でグラフの概形を考えて推測するとよいです。

【解法 1：指数方程式として最大値を見つける】
y = -4^x+1 + 2^x+2
= -4 × 4^x + 4 × 2^x…(1)

2^x = X とおけば、4^x = X² なので (1) は
(1) = -4X² + 4X
= -4(X² – X)
= -4(X – 1/2)² + 1 と平方完成することで
X = 1/2 の時、最大値 1 をとるとわかります。

以上より、正解は 1 です。

【解法 2：グラフの概形を書いて推測する】

x = 0 の時、y = 0 です。
x = -1 の時、y = 1 です。
x = 1 の時、y = -8 です。

3 点結んでグラフの概形を考えます。少し形がわかりづらい印象であれば、x = -2 の時、y = 3/4 も加えるとより概形をつかみやすいと思われます。

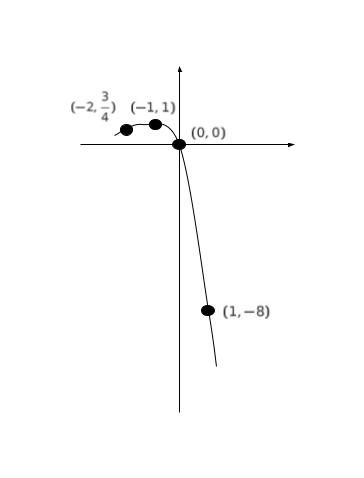
最大値をとりそうな範囲について、もう少し具体的に
x = -1.5 の場合を考えると
y = -1/2 + √2 ≒ -0.5 + 1.4 = 0.9 < 1 です。

グラフの概形から 最大値 2 までは大きくならないようです。選択肢より最大値は 1 と推測されます。

以上より、正解は 1 です。