公務員試験 2023年 国家一般職(土木) No.2 解説

　問 題　　　　　

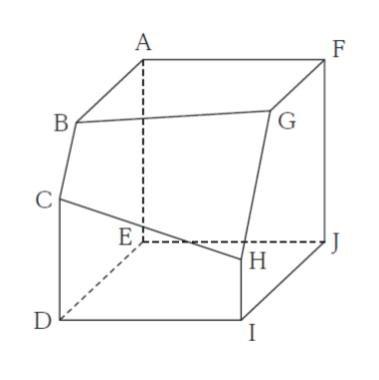
図のように、一辺の長さが 6 の立方体を一つの平面で切り取ってできた立体がある。AB = 5、CD = 4、FG = 4、HI =2 であるとき、この立体の体積はいくらか。

1． 196
2． 198
3． 200
4． 202
5． 204

 

 

 

 

 

　解 説　　　　　

１辺 6 の立方体の体積は 6³ = 216 です。切り取られた立体の体積を 216 から引いたものが答えです。立方体の外枠を点線で書き込むと、切り取られた立体が把握しやすいと思われます。切り取られた立体は三角錐を底面と平行に切断した三角錐台です。

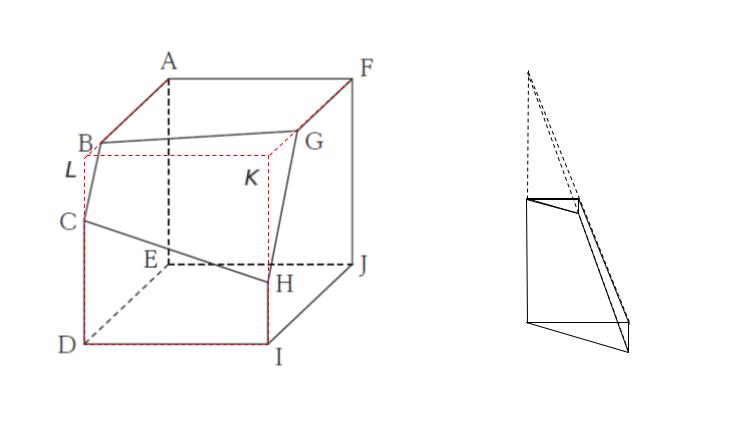
△ GKH の面積は (GK × KH)/2 です。
GK = 6 – FG = 6 – 4 = 2
KH = 6 – HI = 6 – 2  = 4 なので、△ GKH の面積は 4 です。

△ BLC の面積は (BL × LC)/2 です。
BL = 6 – AB = 6 – 5 = 1
LC = 6 – CD = 6 – 4 = 2 なので、△ BLC の面積は 1 です。

△ GKH と △ BLC の面積比が 4：1 なので、相似比が 2：1 です。つまり、切り取られた図形は「大きな三角錐をちょうど真ん中で切断した錐台」であることがわかります。

大きな三角錐の体積は 4 × 12 × 1/3 = 16 です。小さな三角錐の体積は 1 × 6 × 1/3 = 2 です。錐台の体積は 大きな三角錐 ー 小さな三角錐なので 16 – 2 = 14 です。

従って
216 – 14 = 202 が求める体積です。

以上より、正解は 4 です。