問 題
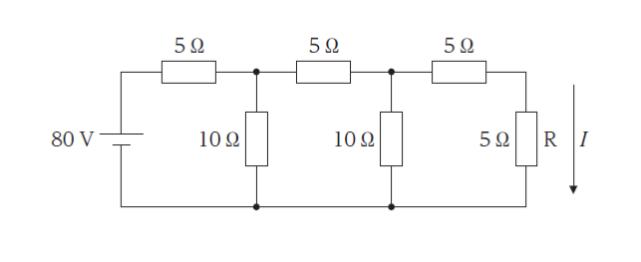
図のような回路において、抵抗 R に流れる電流 I の大きさとして最も妥当なのはどれか。
1. 1 A
2. 2 A
3. 3 A
4. 4 A
5. 5 A
解 説
図の回路は、以下のように書き換えることができます。
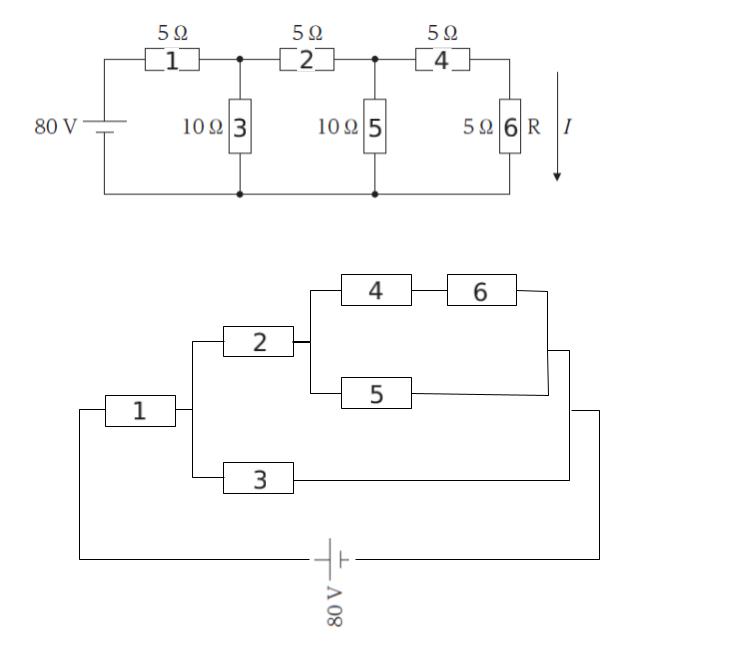
4,5,6 の部分ですが
抵抗 4 と 抵抗 6 がそれぞれ 5 オームで直列なので、合成すれば 10 Ω です。従って、10 Ω と 10 Ω の並列と見なせます。並列抵抗の合成は「分母は足す、分子はかける」です。10・10/(10 + 10) = 5 Ω となります。
抵抗 2,3 及び先程まとめた 5 Ω の部分ですが
抵抗 2 が 5 Ω、抵抗 3 が 10 Ω なので、結局 10 Ω と 10 Ω の並列と見なせます。合成すれば 5 Ω です。
抵抗 1 と、これまでまとめた 5 Ω が直列なので、5 + 5 = 10 Ω です。従って、全体の合成抵抗は 10 Ω とわかりました。
オーム の法則より 流れる電流は 80 = 10 × I から、I = 8 A です。
並列回路では、流れる電流は抵抗の逆比です。そのため、抵抗 1 を 8A が流れた後、4A、4A に分かれます。(抵抗 2,4,5,6 をまとめると 10 Ω です)。そして、抵抗 2 を 4A が流れた後、2A,2A に分かれます。以下のようにまとめられます。
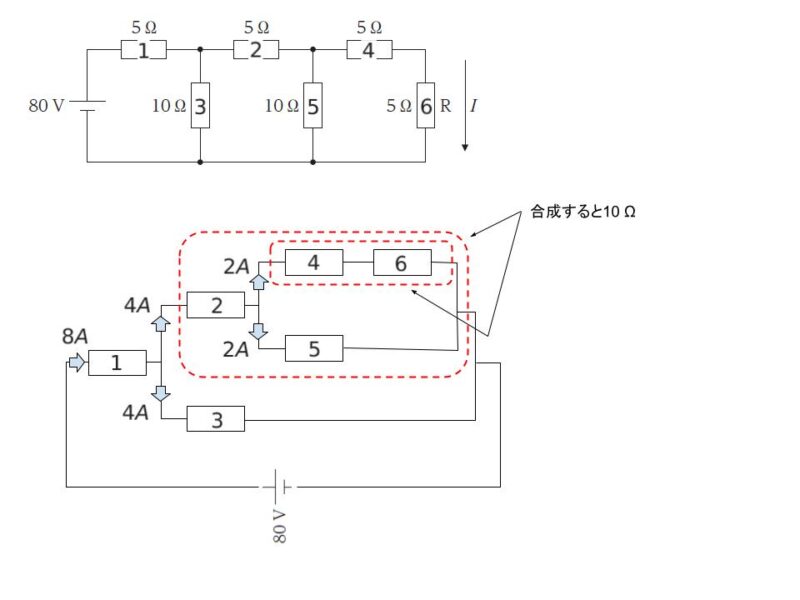
従って
抵抗 R、図の抵抗 6 に流れる電流は 2 A となります。
以上より、正解は 2 です。
参考:本問は「はしご型回路」と呼ばれる形です。合成抵抗を求める際は 1 段ずつ処理していってもよいです。
まず、80 V 側の 5 Ω と、下に降りる 10 Ω の抵抗のみの 1 段だった場合を考えます。直列で 15 Ω と合成できます。
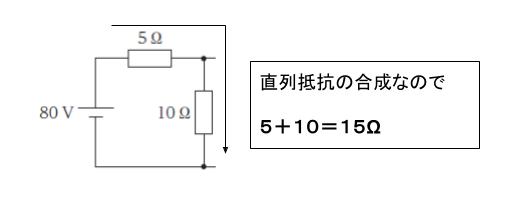
次に 2 段の場合は、まず 5 Ω で、残りは「10 Ω と 15 Ω の抵抗が並列につながっている」と考えます。以下のようなイメージです。
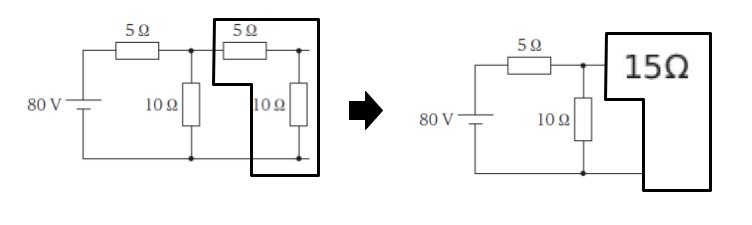
並列抵抗の合成は「分母は足す、分子はかける」です。5 + 10・15/(10 + 15) = 5 + 6 = 11 Ω です。
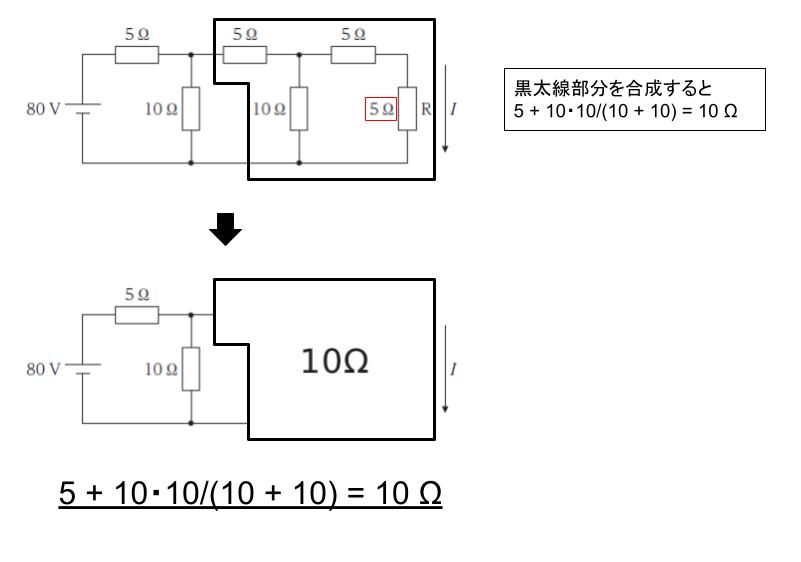
3 段の場合ですが、抵抗 R が 10 Ω ではないことに気をつけます。
先に電源から遠い 2 段分のはしご型回路の合成抵抗を考えます。まず 5 Ω で、10 Ω,10 Ω の並列となるため、並列を合成すると 5 Ω です。つまり 5 + 5 = 10 Ω となります。従って、以下のようにまとめることができます。全体の合成抵抗は 10 Ω とわかります。

コメント