問 題
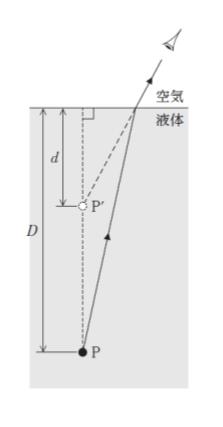
図のように、屈折率が n の液体において液面から深さ D の位置にある小物体 P を、P の真上からわずかにずれた空気中の 1 点から見ると、光の屈折により、P が液面から深さ d の位置に浮き上がって見えた。
このとき、D として最も妥当なのはどれか。ただし、空気の屈折率を 1 とする。なお、角度 θ が十分小さいとき、tanθ ≒ sinθ が成り立つ。
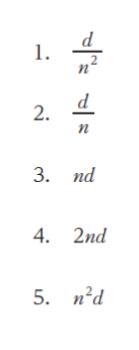
正解 (3)
解 説
【屈折に関する 基礎知識】
媒質1 → 媒質2の時、スネルの法則より、屈折率をそれぞれ n1、n2 とし、入射角 = θi、屈折角 = θr とすると、n1 sinθi = n2 sinθr です。
※ 添字の i,r はそれぞれ入射:incidence (らしいんですが insert の方が思い出しやすいかも)、屈折:refrection の頭文字です。
本問では空気の屈折率が 1 と与えられているので、n1 = 1、n2 を改めて n とすれば sin θi = n sinθr ∴ n = sin θi/sin θr と表せます。
「入射角 θi、屈折角 θr と等しい角を含む直角三角形 2 つ」に注目します。等しい辺に注目すれば、d tan θi = Dtan θr です。∴ D = d tan θi/tan θr です。
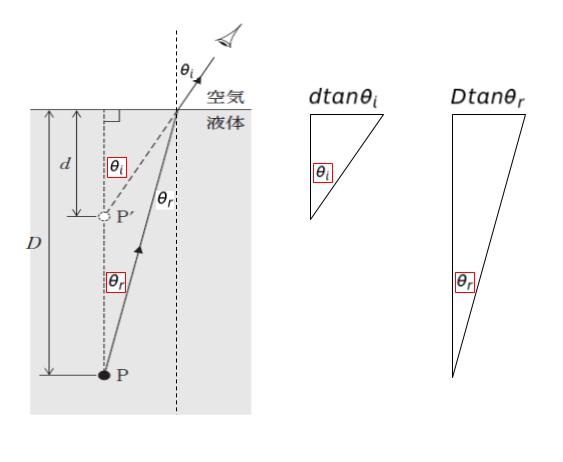
θ は十分小さいので、tan を sin に書き換えれば、tan θi/tan θr = sin θi/sin θr = n です。
従って
D = nd と表せます。
以上より、正解は 3 です。

コメント