問 題
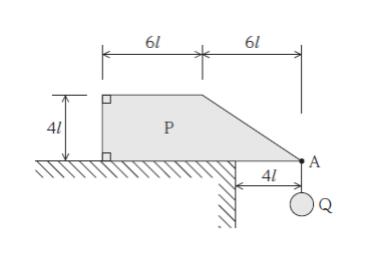
図のように、質量 M の一様な剛体 P を水平な台から長さ 4l だけはみ出すように置き、P の右下端 A から質量 m の小物体 Q を糸でつるした。このとき、P が傾かない最大の m として最も妥当なのはどれか。ただし、P の奥行き方向の厚さは無視できるものとする。また、P と Q は同一の平面内にあり、この平面内における力の釣合いのみを考えるものとする。
なお、必要ならば、三角形の 3 本の中線は 1 点で交わり、各中線はその交点でそれぞれ 2:1 に内分されることを用いてよい。
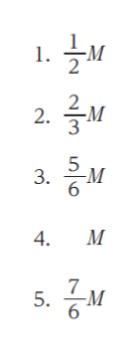
正解 (3)
解 説
問題文に三角形についての但し書きがあることをふまえ、剛体 P を以下のように2つの部分に分割します。剛体全体の質量が M なので、それぞれの 部分の質量は 2M/3、M/3 です。それぞれの重心に、「各部分の質量 × g」の下向きの力がかかります。
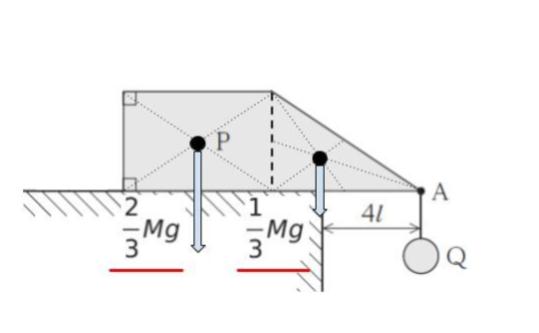
同一平面内なので、本問は単純化して、以下のような問題と考えることができます。
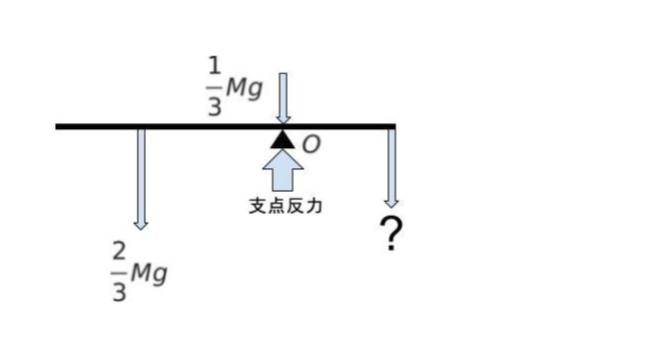
点 O まわりのモーメントに注目します。
・力 2Mg/3 による、↺(反時計回り)モーメントの大きさは
2Mg/3 × 5l = 2Mgl ・・・ (1) です。
球 Q の質量を x とおけば、下向き xg の力がかかっています。力 xg による、↻(時計回り)モーメントの大きさは、x × 4l です。質量 x = 5M/6 の時に (1) とちょうど等しくなり、それより大きくなると傾きます。
以上より、正解は 3 です。

コメント