問 題
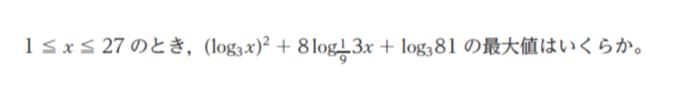
1.-2
2.-1
3. 0
4. 1
5. 2
解 説
【指数・対数の基礎知識】
まず、指数が「数字の肩に乗ってる小さな数」です。23 の「3」が指数の例です。そして対数は、指数部分の別表現です。「log 底真数」という表現をします。
先程の 23 の 指数部分である「3」 を、対数表現すると log28 です。底は「もともとなんていう数字に乗っかってたか」です。2の肩にのっかってたんだから 底が 2 です。真数は「結局全体として、数がいくつか」です。23 = 8 だから、真数が8です。
本問は 「(log3x)2 + 8log1/93x + log381 の最大値」が問われています。まず、log381 = 4 です。この部分は定数です。そのため (log3x)2 + 8log1/93x の最大値を考えればよいです。そこで y = (log3x)2 + 8log1/93x とおきます。
ここから最大値をみつける方法を、以下 2 つ解説します。
【方法 1:底の変換公式等を用いる】
各項で底が異なるため、底を 3 に揃えて整理します。底の変換公式は以下の通りです。
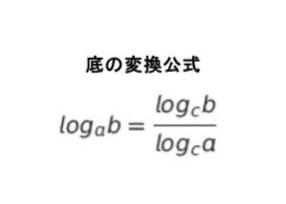
整理して log3x = X (0 ≦ X ≦ 3) とおけば、y = X2 – 4X – 4 となります。
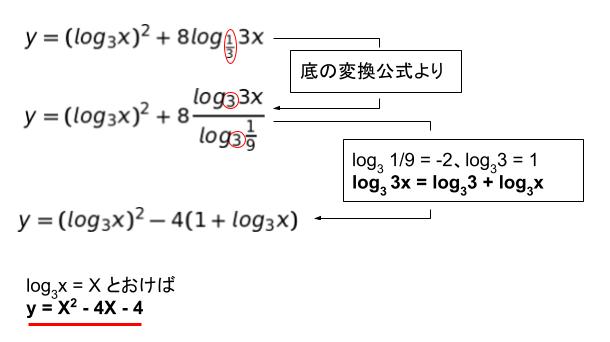
この 2 次関数は X = 2 の時最小値をとるので、0 ≦ X ≦ 3 の範囲で最大値をとるのは X = 0 の時です。つまり x = 1 の時に最小値をとります。元の式に x = 1 を代入すれば、02 + 8 × (-1/2) + 4 = 0 です。
以上より、正解は 3 です。
【方法 2:グラフの概形から推測 おすすめ】
y = (log3x)2 + 8log1/93x とおきます。対数部分の計算がしやすい値として、30、31… を代入します。
・x = 1 を代入します。
02 – 8 × 1/2 = -4 です。
・x = 3 を代入します。
12 +8 × -1 = -7 です。
・x = 9 を代入します。
22 + 8 × (-3/2) = -8 です。
・x = 27 を代入します。
32 + 8 × (-2) = -7 です。
グラフの概形は以下の通りです。
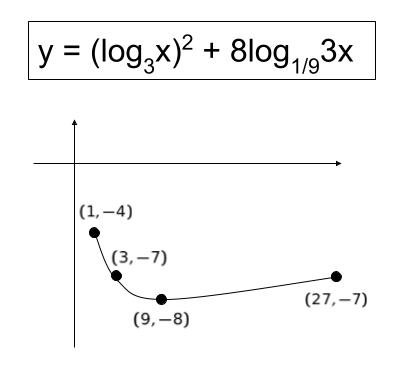
x = 1 の時が最大値と推測されます。元の式に x = 1 を代入すれば、02 + 8 × (-1/2) + 4 = 0 です。
以上より、正解は 3 です。

コメント