問 題
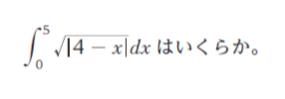
1. 4
2. 6
3. 8
4. 10
5. 12
正解 (2)
解 説
グラフの概形を書き、選択肢を検討するのがおすすめです。
y = √|4 – x| とおきます。
x = 0 の時、y = 2 です。(0,2) を通ります。
x = 1 の時、y = √3 です。(1,√3) を通ります。√3 ≒ 1.7 です。
x = 2 の時、y = √2 です。(2,√2) を通ります。√2 ≒ 1.4 です。
また
特徴的な点として、x = 4 の時、y = 0 です。
そして
絶対値の中身が負になるので、もう 1 点考えておきます。
x = 5 の時、y = 1 です。(5,1) を通ります。
点を滑らかにつなぎグラフの概形を考えます。また、面積の概算のため、三角形で近似した図形を書き込んでいます。
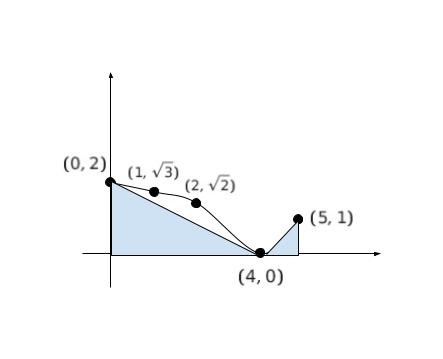
求める面積は、三角形の面積が 4 + 1/2 = 4.5 なので、4.5 より少し大きい値と推測できます。選択肢から最も近い値を選べば 6 です。
以上より、正解は 2 です。
【おすすめしない解法:積分で計算】
絶対値を外して各項を積分すれば、以下の通りです。
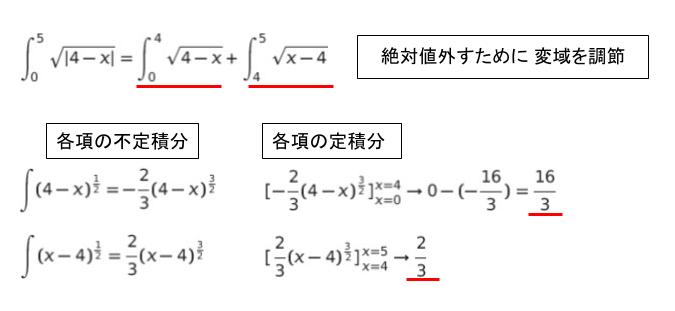
16/3 + 2/3 = 18/3 = 6 です。
以上より、正解は 2 です。

コメント