公務員試験 2022年国家一般職(土木) 工学に関する基礎 No.2 解説

　問題　　　　　

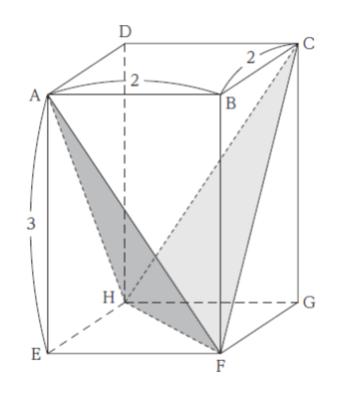
図のような AB = BC = 2，AE = 3 の直方体 ABCD ‒ EFGH において，平面 AFH と平面 CFH のなす角を θ (0 ≦ θ ≦ π/2) とするとき、cosθ の値はいくらか。

正解 (2)

　解説　　　　　

「2 つの平面のなす角」について知らなかった人も多いのではないでしょうか。

まず、2 つの平面は平行でなければ交わって「交線」ができます。本問では HF が対応します。交線上の適当な点から、2 平面方向に「交線と垂直」な線を引き、2 直線のなす角が「2 つの平面のなす角」です。

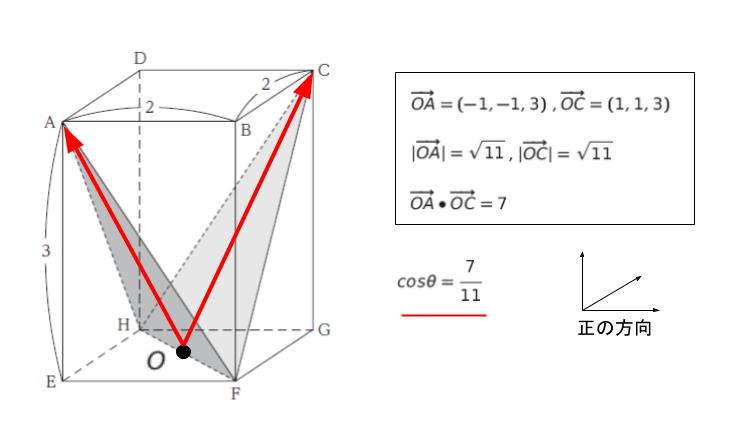
本問では HF の中点を O として、OA と OC のなす角と考えるのがわかりやすいと思われます。cos θ が聞かれているため、ベクトルの内積を考えます。以下の公式は基礎知識です。

ベクトル、大きさ、内積はそれぞれ以下の通りです。従って、cos θ = 7/11 です。ベクトルの正負については各自のやりやすい方向でかまいません。

以上より、正解は 2 です。

コメント