公務員試験 2021年 国家一般職(土木) 工学に関する基礎 No.13 解説

　問 題　　　　　

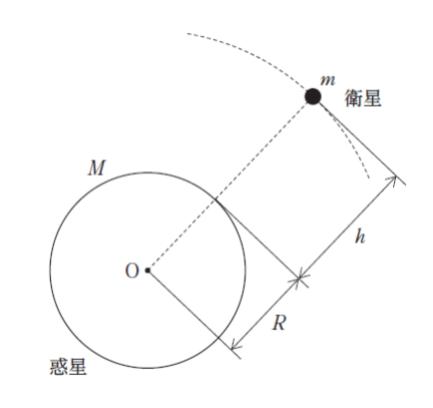
図のように、質量 m の衛星が、半径 R、質量 M の球形の惑星の周りを、惑星の地表面から高さ h で等速円運動している。惑星の地表面における重力加速度の大きさを g とするとき、この等速円運動の周期として最も妥当なのはどれか。

ただし、衛星の大きさ、惑星の自転及び公転の影響、他の天体の影響は無視できるものとし、惑星の密度は一様で全質量が中心 O に集中しているとみなせるものとする。なお、質量が m₁、m₂ の物体が距離 r 離れているとき、 2 物体間に働く万有引力の大きさ F は、F = Gm₁m₂/r² (G は万有引力定数) である。

 

 

 

 

 

　解 説　　　　　

【万有引力の基礎知識】
万有引力の公式 F = Gm₁m₂/ r² は基本公式です。与えられなくても覚えておく方がよいです。

※地表面において  F = mg であることから、地球の質量を M、地球の半径を R とおけば「GM = gR²」が成り立ちます。本問では、惑星について GM = gR² です。万有引力の公式に関連して、ここまでが基本知識となります。

衛星が等速円運動をしているとあります。円運動が出てきたら遠心力を考えます。「 F_遠心力=mrω² = mv²/r 」です。本問における r = (R + h) です。本問では「円運動の周期」、つまり 1 周するまでの時間が問われているため 角速度 ω の方の式を使います。1 周 = 2π なので、周期は 2π/ω です。

遠心力 m(R+h)ω² と、惑星ー衛星 間の万有引力 GmM/(R+h)² が等しいので m(R+h)ω² = GmM/(R+h)² …(1) です。「◯/ω = …」に変形していきます。以下は変形の一例です。

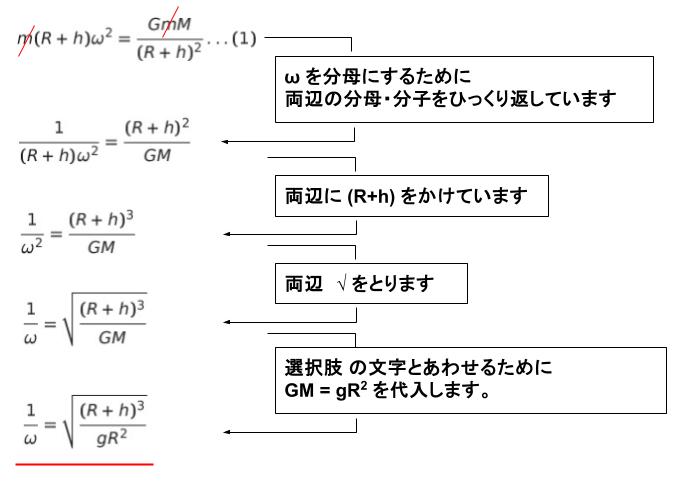
最後の式の両辺に 2π かければ周期です。

以上より、正解は 4 です。

類題 H27 no12
https://yaku-tik.com/koumuin/h27-doboku-12/