問 題
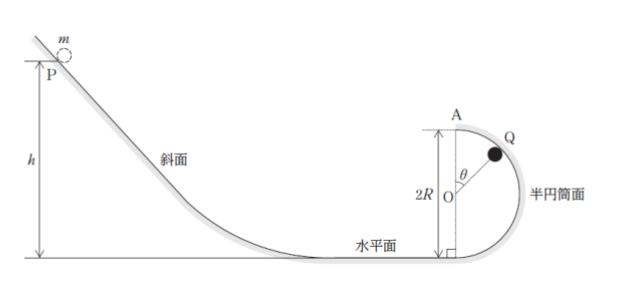
図のように、斜面、水平面、半径 R の半円筒面が滑らかに接続されており、半円筒面の上端に点 A をとる。水平面からの高さが h (h > 5R/2) である斜面上の点 P から、質量 m の小球を静かに滑らせた。
半円筒面の中心軸と鉛直面との交点を O とし、∠AOQ = θ (0 ≦ θ ≦ π) となる半円筒面上の点 Q に小球があるとき、小球の速さと小球が半円筒面から受ける垂直抗力の大きさの組合せとして最も妥当なのはどれか。
ただし、重力加速度の大きさを g とし、A、O、P、Q は同一鉛直面上にあるものとする。また、小球と斜面、水平面、半円筒面の間の摩擦はないものとする。

解 説
【小球の速さ】
θ = π の時を考えます。この時の小球の速さは「斜面を降りきった時の速さ」と同じです。力学的エネルギー保存則から mgh = mv2/2 より、v = √2gh です。
θ = π の時、cos θ = -1 なので、選択肢の ( ) の中身は「(h – R – Rcosθ)」が妥当です。(h – R + Rcosθ) では、θ = π の時に √2gh になりません。正解は 3 ~ 5 です。
【垂直抗力の大きさ】
θ = 0 の時を考えます。
円運動なので、遠心力 F = mv2/R が上向きに作用します。
※ここで、小球の速さ v は 選択肢 より √2g(h – R – R) = √2g(h – 2R) です。従って、v2 = 2g(h – 2R) です。遠心力 F = 2mg(h – 2R)/R です。
質量 m なので、下向きに mg の力が作用します。
また、垂直抗力を N とおけば N も下向きに作用します。
N + mg = 2mg(h – 2R)/R となるため
N = mg(2h/R – 5) です。
選択肢の中で、θ = 0、つまり cos θ = 1 の時に
N = mg(2h/R – 5) となるのは 「mg(2h/R – 2 – 3cosθ)」です。
以上より、正解は 5 です。

コメント