公務員試験 2021年 国家一般職(土木) 工学に関する基礎 No.11 解説

　問 題　　　　　

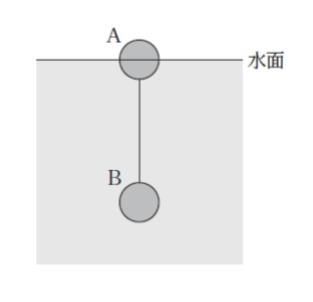
図のように、体積が等しくそれぞれ均質な二つの球 A、B をロープでつないで水に入れたところ、A の体積のちょうど半分が水面から上に出た状態で、ロープがたるまずに浮かんだ。この状態から、ロープを静かに切ったところ、B は下降し始めた。

水の密度が ρ、A の密度が ρ/4 であるとき、B の密度 ρ_B とロープを切った瞬間の B の加速度の大きさ α_B の組合せとして最も妥当なのはどれか。ただし、重力加速度の大きさを g とし、空気による浮力、ロープの質量と体積は無視できるものとする。

 

 

 

 

 

　解 説　　　　　

液体があるので浮力を考えます。浮力は「体積 × 液体の密度 × g」です。また、密度が出てきているので、質量 m = Vρ を意識します。小球 A,B の体積を V とおきます。

本問は、小球が 2 つ、液体もひももあるという設定で、状況がやや複雑です。こういう場合は 1 つずつの物に注目するとよいです。

【物体 A に作用する力】
・質量 V × (ρ/4) なので、下向きに V × (ρ/4) × g…(1) の力が作用します。
・半分水面に沈んでいるので、上向きに (V/2) × ρ × g…(2) の浮力が作用します。
・ひもから下向きに 張力 T…(3)  が作用します。

ちょうどこれで静止しているので
(1),(2),(3) の和が 0 です。従って、T = V × (ρ/4) g 下向きとわかります。張力は同じひもであれば等しいため、小球 B を上向きに引っ張る力も V × (ρ/4) g です。

【物体 B に作用する力】
・質量 V × (ρ_B) なので、下向きに V × (ρ_B) × g…(4) の力が作用します。
・水面に沈んでいるので、上向きに (V) × ρ × g…(5) の浮力が作用します。
・ひもから上向きに 張力 T = V × (ρ/4) g…(6) が作用します。

(4),(5),(6) の和が 0 なので
ρ_B = 5ρ/4 です。正解は 1 or 2 です。

【ロープを切った瞬間に作用する力と加速度】
ひもからの力が伝わらなくなるので、(4),(5) の和である 下向きに (ρ/4) × Vg…(7) の力が作用します。F = ma より、a = F/m です。小球 B の質量は V × (5ρ/4)…(8) なので、(7) ÷ (8) = g/5 です。

以上より、正解は 1 です。