公務員試験 2021年 国家一般職(土木) 工学に関する基礎 No.10 解説

　問 題　　　　　

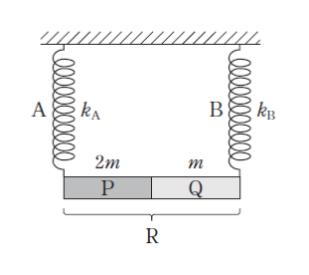
質量 2m の一様な剛体棒 P と、長さ及び断面形状が P とそれぞれ同じで、質量 m の一様な剛体棒 Q を隙間なく接合した剛体棒 R がある。

図のように、R の両端を、水平な天井の 2 点から軽いばね A、B が鉛直になるようにつるしたところ、A、B は同じ長さとなった。A、B の自然長が等しいとき、A、B のばね定数 k_A、k_B の比として最も妥当なのはどれか。

 

 

 

 

 

　解 説　　　　　

剛体棒 P は質量 2m なので、下向き 2mg の力が作用します。
剛体棒 Q は質量 m なので、下向き mg の力が作用します。

ばね A、ばね B が棒を支え、上向きの力が作用します。これらを F_A、F_B とおきます。図に書き込むと以下のようになります。棒 R の長さを R としています。

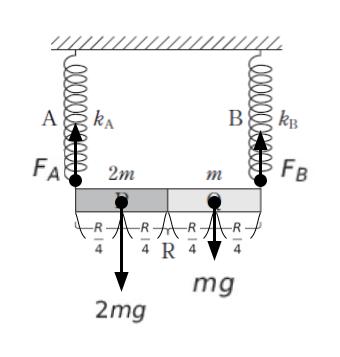
棒の左端を中心としたモーメントを考えます。

・下向きの力 2mg により、2mg × R/4 (時計回り)
・下向きの力 mg により、mg × 3R/4 (時計回り)

・上向きの力 F_B により、F_B × R (反時計回り)

これらの和が 0 と考えられます。従って、F_B = 5mg/4 です。

同様に、棒の右端を中心としたモーメントを考えます。

・下向きの力 mg により、mg × R/4 (時計回り)
・下向きの力 2mg により、2mg × 3R/4 (時計回り)

・上向きの力 F_A により、F_A × R (反時計回り)

これらの和が 0 と考えられます。従って、F_A = 7mg/4 です。

ばねなので、フックの法則：F = kx を思い出します。自然長からの伸び x がばね A,B で等しいため、F の違いはそのまま k の違いです。F_A：F_B = k_A：k_B = 7 : 5 です。

以上より、正解は 4 です。