公務員試験 2021年 国家一般職(土木) 工学に関する基礎 No.9 解説

　問 題　　　　　

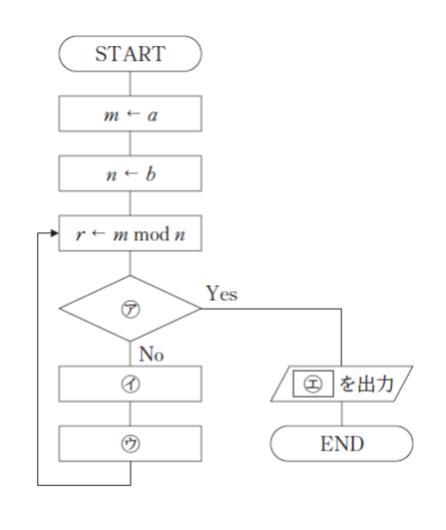
図は、二つの自然数 a、b (a ≧ b) の最大公約数を出力する処理を表すフローチャートである。

二つの自然数 X、Y (X ≧ Y) において、X を Y で割ったときの余りを R とすると、X と Y の最大公約数は、Y と R の最大公約数に等しい。この性質を用いると、次の操作 ①、②、③ を行うことで、X と Y の最大公約数を求めることができる。

① X を Y で割ったときの余りを R とする。

②  R ≠ 0 のとき、Y の値を X に、R の値を Y に代入して ① に戻る。R = 0 のとき、③ へ進む。

③ このときの Y が最大公約数である。

図中の ㋐ ～ ㋓ に当てはまるものの組合せとして最も妥当なのは次のうちではどれか。ただし、A mod B は、A を B で割ったときの余りを表す。

 

 

 

 

 

　解 説　　　　　

㋐ ですが
「R = 0 の時に ③ へ進み、その時の Y が求める最大公約数」とあります。チャートにおいて問題文の R は r と対応しています。従って、r = 0 が妥当です。正解は 3 ~ 5 です。

㋑ ですが
R ≠ 0 の場合に「Y の値を X に、R の値を Y に代入」とあります。チャートに置いて問題文の Y は n に、X は m に対応しています。従って、m ← n、n ← r が妥当です。これにより、㋒ は n とわかります。

以上より、正解は 3 です。