問 題
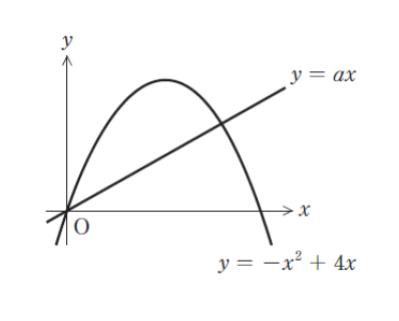

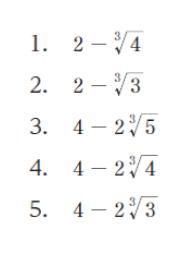
解 説
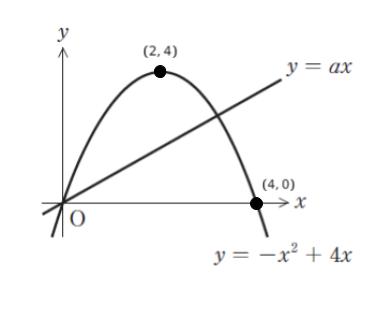
-x2 + 4x = x(-x+4) なので、グラフと x 軸の交点は x = 0,4 です。また、頂点の座標は (2,4) です。頂点の座標は 平方完成しても、微分して y’ = 0 でも、グラフの形から、軸が x = 2 より x = 2 を代入して求めてもかまいません。各点の座標を書き込むと下図です。
【解法 1:問題文のヒントを使って積分】
y = ax と y = -x2 + 4x の交点は
ax = -x2 + 4x
a = -x + 4 ∴ x = 4 – a です。
2 等分された面積の上半分部分は、定積分で表すと以下の通りです。
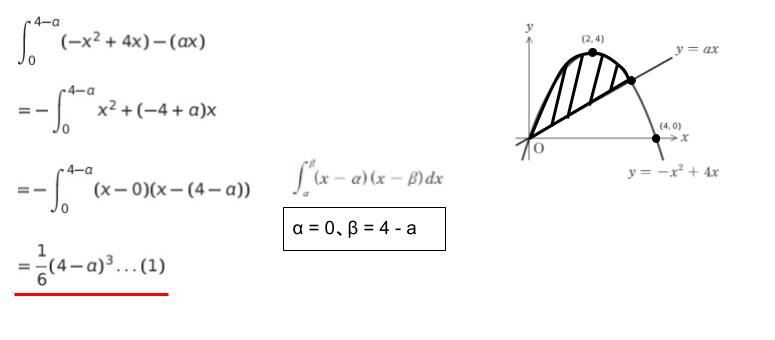
また、単に y = -x2 + 4x を x = 0 ~ 4 まで積分した時は、問題文の関係式より 1/6 × (4-0)3 = 32/3 です。(1) はこの半分なので (1) = 32/6 です。選択肢から a = 4 – 23√4 が答えです。
以上より、正解は 4 です。
【解法2:近似して推測】
放物線と x 軸で囲まれた部分を三角形で近似します。(2,4) と (4,0) の中点 (3,2) と原点を結んだ線で面積が二等分されます。この時直線の傾きは 2/3 です。 次図参照
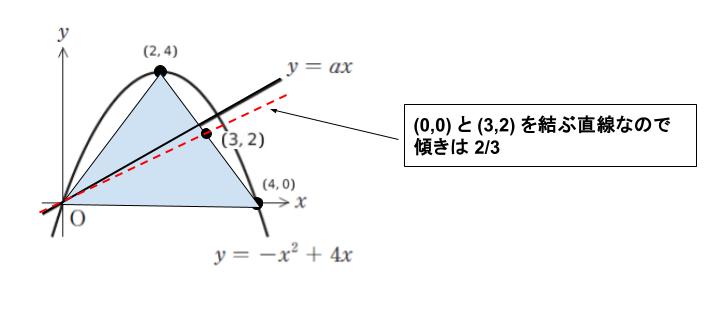
求めたい直線の傾きである定数 a は 2/3 よりも少し大きい数と推測できます。
3√2 ≒ 1.26
3√3 ≒ 1.44
3√4 ≒ 1.59
3√5 ≒ 1.71 より
選択肢 1:2 – 3√4 ≒ 0.4
選択肢 2:2 – 3√3 ≒ 0.6
選択肢 3:4 – 23√5 ≒ 0.6
これらは 2/3 より小さいので誤りです。
選択肢 4:4 – 23√4 ≒ 0.8
選択肢 5:4 – 23√3 ≒ 1
選択肢 5 はやや大きすぎると判断できます。
以上より、正解は 4 です。

コメント