問 題
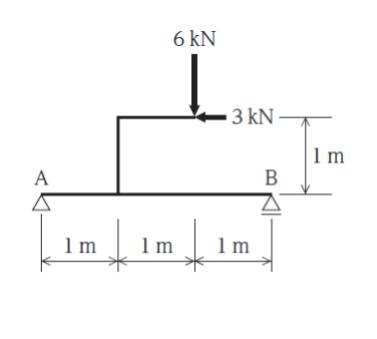
図のような荷重を受ける構造物において、支点 A と支点 B におけるそれぞれの鉛直方向の反力 VA と反力 VB の大きさの組合せとして最も妥当なのはどれか。ただし、部材の自重は無視するものとする。

正解 (3)
解 説
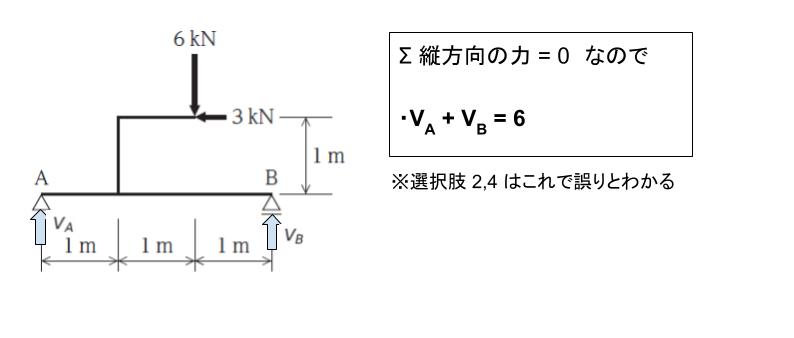
支点反力を求めます。A における垂直反力を VA、B における垂直反力を VB とおきます。集中荷重が下向きに 6 kN かかっています。Σ 縦方向の力 = 0 のはずなので、VA + VB = 6 ・・・(1)です。これにより、選択肢 2,4 は誤りです。
点 A 周りのモーメントを考えます。モーメントは 力 × 距離です。力の作用線を延長させて点 A との距離を考えると、点 A と下向き 6kN の力までの距離は 2m、左向き 3kN の力までの距離は 1m、VB までの距離は 3m です。
下向き 6kN の力によるモーメント:6 × 2 = 12(時計回り)
左向き 3kN の力によるモーメント:3 × 1 = 3 (反時計回り)
VB によるモーメント:VB × 3 (反時計回り) です。
※それぞれの力によるモーメントが時計回りか反時計回りか 少しわかりにくいかもしれません。そこで「力の作用線上であれば、力の効果が変わらない」ことを利用すると判断しやすいと思われます。以下の図は、延長した力の矢印を追記しています。
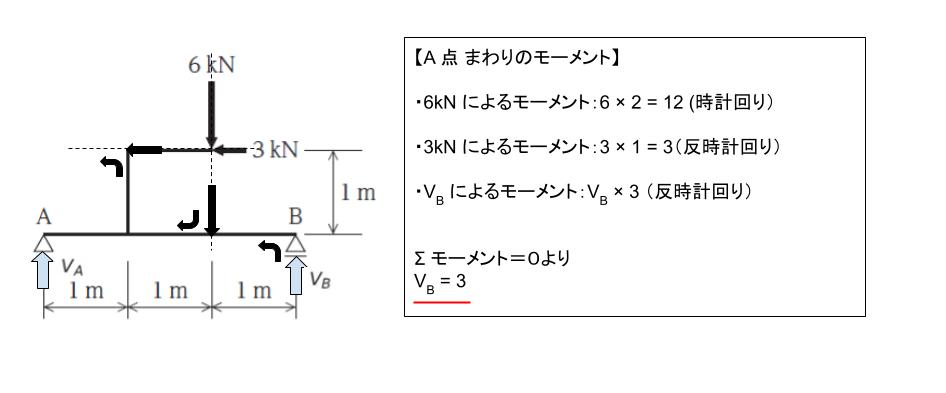
Σモーメント=0より、VB = 3 です。
(1)より、VA = 3 となります。
以上より、正解は 3 です。

コメント