問 題
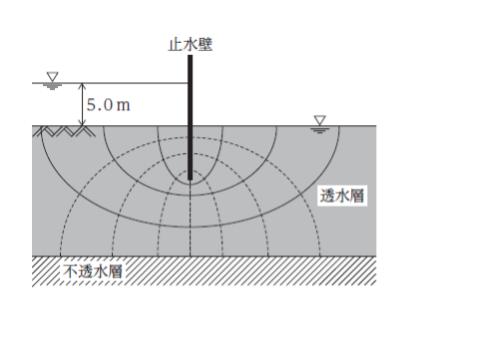
図は、ある地盤の透水層の一部に止水壁を打ち込み、止水しているときの流線網を描いたものである。この透水層の透水係数が 2.0 × 10-4 m/s、水頭差が 5.0 m であるとき、止水壁の下をまわって浸透する単位奥行き(1.0 m)当たりの 1 時間の透水量として最も妥当なのはどれか。
ただし、水位は変化しないものとする。また、単位奥行き(1.0 m)当たりの透水量を q、透水係数を k、水頭差を h、流線ではさまれる帯の数を Nf、等ポテンシャル線ではさまれる帯の数を Nd とすると、次式が成り立つものとする。
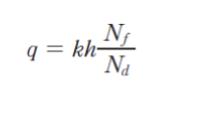

正解 (2)
解 説
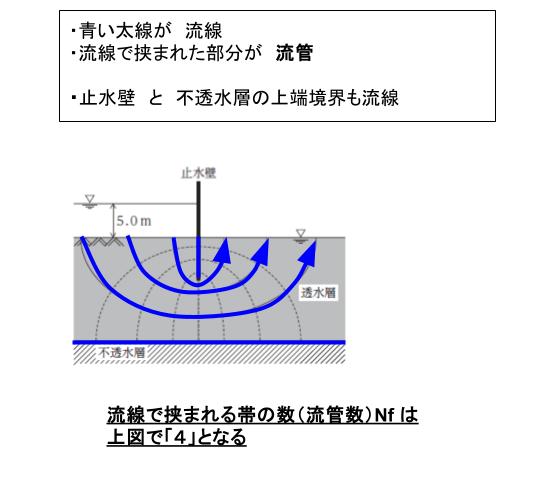
流線網は、浸透する水の流れの経路を示す「流線」と、同じ高さの地点を結ぶ等高線のようなイメージで「全水頭が等しい点を結んだ 等ポテンシャル線」からなる網目状の図のことです。流線で挟まれる部分を流管といいます。
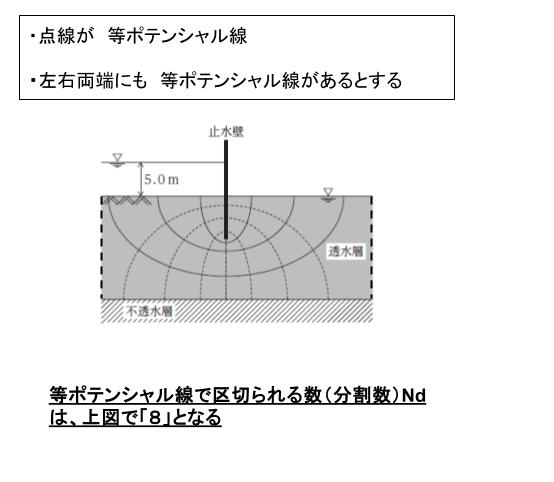
等ポテンシャル線ではさまれる帯の数は分割数 Nd といいます。Nd を図から読み取る時は 左右両端にも 等ポテンシャルがあるものと考えて読み取ります。本問の流線網において、分割数 Nd は「8」です。
従って、問題文より k = 2.0 × 10-4、h = 5 m、流線網より Nf = 4、Nd = 8 なので代入して計算すると、5 × 10-4 (m2/s) です。
m2/s、つまり 1 秒当たりなので、1時間なら 3600 をかけることで 1.8 m2/h となります。選択肢との単位の違いについてですが、q は単位奥行き 1.0 m あたりの透水量なので、1.0 をかけて、数値は変わらず単位は m3 となっています。
以上より、正解は 2 です。

コメント